Hàm số bậc nhất là một trong những chủ đề nền tảng mà học sinh cần nắm vững trong chương trình Toán phổ thông. Bài viết này kpophoto sẽ hệ thống lại kiến thức cốt lõi, đồng thời chia sẻ cách ghi nhớ công thức một cách dễ tiếp thu, khoa học.
Hàm số bậc nhất là gì?
Hàm số bậc nhất được hiểu là hàm có dạng tổng quát y = ax + b với a ≠ 0, trong đó a và b là các hằng số thực, x là biến số. Biểu thức này thể hiện mối quan hệ tuyến tính giữa hai đại lượng, tức là khi một đại lượng thay đổi, đại lượng kia cũng thay đổi theo tỷ lệ cố định.
Một đặc điểm nổi bật của hàm bậc nhất là đồ thị của nó luôn là một đường thẳng trên mặt phẳng tọa độ. Tùy theo giá trị của hệ số a, đường thẳng đó có thể nghiêng lên hoặc nghiêng xuống, biểu thị sự đồng biến hoặc nghịch biến của hàm.

Hàm bậc nhất được sử dụng rộng rãi trong các bài toán Đại số lớp 9, là nền tảng để học các hàm phức tạp hơn ở cấp độ cao hơn. Vì có cấu trúc đơn giản, loại hàm này thường là bước đệm cho học sinh làm quen với cách khảo sát, vẽ đồ thị hàm số.
Khác với hàm hằng số không thay đổi giá trị khi biến đổi x, hàm số bậc nhất phản ứng tức thời với từng thay đổi nhỏ của biến đầu vào. Điều này giúp người học hình dung trực quan hơn về các mối quan hệ tuyến tính trong thực tiễn.
Đặc điểm và tính chất của hàm số bậc nhất
Để hiểu sâu về hàm số bậc nhất, cần phân tích chi tiết từng yếu tố cấu thành, vai trò của chúng trong việc quyết định tính chất hàm. Các nội dung dưới đây sẽ cho thấy rõ ảnh hưởng của hệ số, biểu thức hàm tới hình dạng cũng như xu hướng biến thiên trên đồ thị.
Tính đơn điệu và hệ số góc
Tính đơn điệu của hàm bậc nhất thể hiện qua việc hàm tăng hoặc giảm đều khi x thay đổi. Điều này được quyết định trực tiếp bởi hệ số góc a.
- Nếu a > 0, hàm số đồng biến, tức là giá trị y tăng khi x tăng; ngược lại, nếu a < 0, hàm số nghịch biến, y giảm khi x tăng. Chính hệ số góc đã quy định toàn bộ xu hướng biến thiên của đường thẳng biểu diễn hàm.
- Hệ số góc cũng phản ánh độ nghiêng của đồ thị, nghĩa là càng lớn về độ lớn, đường thẳng càng dốc. Khi a tiệm cận 0, đường thẳng gần như nằm ngang, trong khi nếu a rất lớn hoặc rất nhỏ, đồ thị gần như đứng dốc.
- Ngoài ra, hệ số góc còn có thể được tính từ đồ thị nếu biết hai điểm trên đường thẳng. Công thức tính a = (y₂ – y₁)/(x₂ – x₁) giúp kiểm chứng lại biểu thức hàm từ dữ liệu trực quan.
Điều kiện đồng biến, nghịch biến của hàm số bậc nhất
Một hàm số bậc nhất sẽ đồng biến trên toàn tập xác định nếu hệ số a > 0. Trong trường hợp này, đồ thị hàm luôn đi lên khi nhìn từ trái sang phải. Ngược lại, nếu a < 0, hàm số nghịch biến, biểu thị bằng đồ thị đi xuống khi x tăng.
Giá trị của b không ảnh hưởng tới sự đồng biến hay nghịch biến, mà chỉ làm dịch chuyển đồ thị lên hoặc xuống. Tính chất này giúp học sinh dễ dàng phân biệt các hàm số qua quan sát nhanh đồ thị hoặc qua dạng đại số.
Đồng thời, nó cũng là yếu tố cốt lõi khi xét các bài toán tương quan giữa hai hàm tuyến tính. Dù hàm số được viết dưới nhiều dạng khác nhau, chỉ cần xác định được hệ số a, người học đã có thể kết luận về chiều biến thiên của hàm.
Ảnh hưởng của hệ số a và b đến đồ thị
Hệ số a ảnh hưởng đến độ nghiêng của đồ thị hàm số bậc nhất, xác định tính đồng biến hay nghịch biến của hàm. Khi a đổi dấu, đồ thị quay ngược lại qua trục tung. Trong khi đó, hệ số b quyết định điểm cắt của đồ thị với trục tung, hay chính là giá trị y tại x = 0.
Nó không làm thay đổi hướng của đường thẳng, mà chỉ dịch chuyển đồ thị lên hoặc xuống. Thay đổi a làm xoay đồ thị quanh điểm gốc cắt trục tung, còn thay đổi b đẩy toàn bộ đường thẳng theo chiều thẳng đứng. Nhờ đó, người học có thể dễ dàng hình dung sự biến đổi của đồ thị khi điều chỉnh các hệ số.

Từ hai tham số này, người học có thể vẽ lại nhanh đồ thị mà không cần tính quá nhiều điểm. Khả năng đọc hiểu và thao tác trên hệ số chính là điểm mấu chốt trong việc rèn luyện tư duy hàm số.
Xem thêm: Phương Trình Bậc Hai – Cách Giải Và Ứng Dụng Chi Tiết
Đồ thị của hàm số bậc nhất
Sau khi nắm được tính chất, việc biểu diễn hàm số bậc nhất qua đồ thị giúp người học kết nối giữa công thức, hình ảnh. Đồ thị không chỉ hỗ trợ trực quan mà còn đóng vai trò quan trọng trong việc giải bài toán ứng dụng. Cụ thể như kpophoto chia sẻ sau:
Cách xác định hai điểm để vẽ đồ thị
Để vẽ một đường thẳng, chỉ cần xác định hai điểm phân biệt. Với hàm số y = ax + b, ta thường chọn hai giá trị bất kỳ của x, rồi thay vào biểu thức để tìm y tương ứng.
Phổ biến nhất là chọn x = 0 và x = 1 để tiết kiệm thời gian tính toán. Điểm đầu tiên (0; b) luôn là giao điểm với trục tung, giúp định hướng nhanh hình dạng đường thẳng. Sau khi xác định hai điểm, nối chúng lại ta được đường thẳng biểu diễn hàm số bậc nhất.
Càng chính xác ở khâu chọn điểm, đồ thị càng đúng, dễ nhìn. Đôi khi trong các bài toán nâng cao, cần xác định thêm các điểm đặc biệt, như điểm cắt trục hoành, tức điểm y = 0, để làm rõ cấu trúc hàm. Nhưng với hàm bậc nhất cơ bản, hai điểm là đủ.
Vị trí đường thẳng so với trục hoành và trục tung
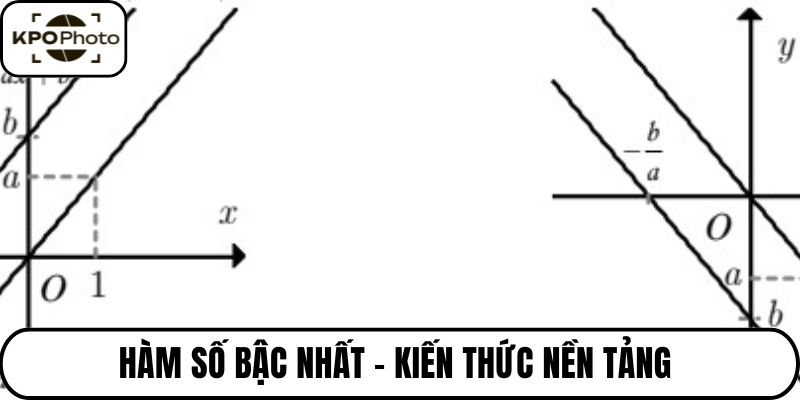
Vị trí của đồ thị hàm số bậc nhất so với trục tọa độ phụ thuộc vào hệ số a và b. Nếu a > 0, đường thẳng nghiêng lên; nếu a < 0, nó nghiêng xuống; còn nếu b = 0, đồ thị đi qua gốc tọa độ.

Đường thẳng sẽ cắt trục hoành tại điểm có tọa độ (-b/a; 0), cắt trục tung tại điểm (0; b). Hai điểm này cung cấp góc nhìn toàn diện về vị trí đồ thị trong mặt phẳng. Việc hiểu rõ vị trí giúp người học nhận diện nhanh được dạng đồ thị mà không cần vẽ chi tiết. Đây là kỹ năng cần thiết khi làm bài thi trắc nghiệm tốc độ cao.
Bên cạnh đó, mối quan hệ giữa các hàm số còn có thể xét qua vị trí tương đối giữa các đường thẳng: song song, cắt nhau hoặc trùng nhau. Điều này thường xuất hiện trong bài toán hệ phương trình.
Đồ thị mẫu thường gặp cùng cách ghi nhớ công thức
Một số đồ thị mẫu học sinh thường gặp là các hàm y = x, y = -x + 2, y = 2x – 1, y = -3x… Những hàm này có hệ số đơn giản, dễ nhận diện hình dạng. Thông qua việc phân tích các ví dụ trên, người học có thể rèn khả năng xác định nhanh hướng, điểm cắt, mối quan hệ với trục tọa độ.
Đó là bước chuẩn bị tốt cho các bài toán phức tạp hơn. Các bài tập dạng này thường yêu cầu học sinh nhận biết dạng đồ thị từ công thức, hoặc ngược lại – xác định biểu thức từ đồ thị. Tư duy hai chiều này rất quan trọng trong kiểm tra và thi cử.
Khi luyện tập nhiều dạng đồ thị mẫu, học sinh có thể linh hoạt áp dụng vào những dạng toán khó hơn như bài toán tìm điều kiện để hai hàm cắt nhau tại điểm có hoành độ xác định.
Kết luận
Hàm số bậc nhất không chỉ là kiến thức cơ bản trong môn Đại số mà còn là nền tảng cho các hàm số phức tạp hơn. Việc nắm chắc định nghĩa, cấu trúc hàm, cùng các đặc điểm về tính biến thiên và đồ thị mà kpophoto chia sẻ sẽ giúp học sinh tự tin hơn khi giải toán.