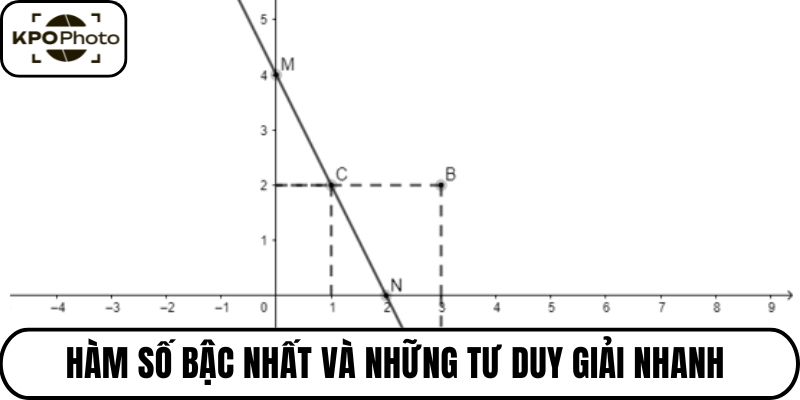
Hàm số bậc nhất là chủ đề quan trọng trong chương trình đại số, xuất hiện trong hầu hết các bài toán từ cơ bản đến nâng cao. Bài viết này, kpophoto sẽ hệ thống kiến thức trọng tâm, đồng thời hướng dẫn tư duy giải quyết vấn đề một cách logic và sáng tạo.
Khái niệm và đặc điểm của hàm số bậc nhất (HSBN)
Hàm có dạng tổng quát là y=ax+b, trong đó a ≠ 0. Đây là biểu thức tuyến tính, đại diện cho mối quan hệ tỉ lệ tuyến tính giữa hai biến.
- Điểm đặc trưng của hàm số này là đồ thị luôn là một đường thẳng trên mặt phẳng tọa độ. Độ dốc của đường thẳng phụ thuộc vào hệ số aaa, xác định xu hướng tăng hay giảm của hàm.
- Hệ số b điều chỉnh vị trí của đồ thị theo trục tung mà không làm thay đổi độ dốc. Khi a>0, hàm đồng biến; ngược lại, a<0 cho ta một hàm nghịch biến.
- HSBN xác định với mọi giá trị thực của biến x, do đó tập xác định luôn là R. Ngoài ra, hàm có tính liên tục trên toàn trục số.
Từ đồ thị, ta có thể suy ra nhiều đặc điểm như chiều biến thiên, điểm cắt trục hoành, tung. Những đặc điểm này giúp rút ngắn thời gian phân tích trong bài tập trắc nghiệm.
Tư duy giải nhanh bài toán hàm số bậc nhất
Trong các kỳ thi, tốc độ giải quyết bài toán HSBN đóng vai trò then chốt. Do đó, rèn luyện tư duy phản xạ nhanh với từng dạng là chiến lược hiệu quả.
Nhận dạng nhanh dạng bài qua đề thi
Hầu hết bài toán liên quan đến HSBN đều có biểu hiện cụ thể qua dạng phương trình tuyến tính. Nhìn vào cấu trúc y=ax+b, học sinh cần phát hiện nhanh hệ số để nhận diện.
Ví dụ điển hình là bài toán về xác định chiều biến thiên hoặc tìm hoành độ giao điểm. Trong trường hợp này, quan sát nhanh hệ số aaa giúp đưa ra kết luận tức thì.
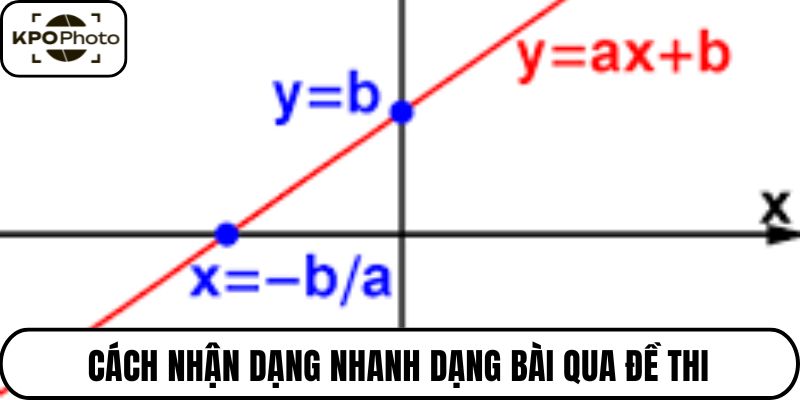
Đề thi thường biến tấu yêu cầu, nhưng nếu nắm được dấu hiệu như hệ số âm hay dương, điểm giao trục, thì quá trình phân tích sẽ nhanh hơn. Những biểu thức kèm điều kiện cũng cần được xử lý gọn gàng bằng phương pháp thế nhanh.
Việc luyện tập thường xuyên các dạng đề phổ biến cũng tăng khả năng phản xạ. Học sinh nên lập bảng nhận dạng các đặc điểm quen thuộc để tiết kiệm thời gian phân tích.
Mẹo xử lý bài toán tương giao, tìm tập xác định
Tìm điểm tương giao giữa hai hàm số thực chất là bài toán giải phương trình hoán vị. Khi làm nhanh, ta chỉ cần đặt hai biểu thức bằng nhau, giải phương trình bậc nhất đơn giản.
Ví dụ: y=2x+1 và y=−x+4, thì hoành độ giao điểm chính là nghiệm của 2x+1=−x+4. Kết quả này cho biết cả hai đồ thị cắt nhau tại một điểm cụ thể.Tập xác định của HSBN luôn là tập số thực.
Tuy nhiên, nếu đề bài thêm điều kiện ràng buộc, cần xét lại để tránh mắc lỗi không đáng có. Các câu hỏi có giới hạn giá trị x sẽ yêu cầu suy luận nhanh từ điều kiện. Thay vì giải từ đầu, hãy kiểm tra trực tiếp các đáp án bằng thử nghiệm nhanh.
Hàm số bậc nhất ứng dụng thực tế làm gì?
Bên cạnh ý nghĩa lý thuyết, HSBN còn có tính ứng dụng rõ rệt trong nhiều lĩnh vực. Đặc biệt, các mối quan hệ tuyến tính trong đời sống thường được biểu diễn dưới dạng này.
Bài toán liên quan đến vật lý, kinh tế
Trong vật lý, chuyển động đều được mô tả bằng hàm số tuyến tính. Vận tốc không đổi dẫn đến quãng đường thay đổi đều theo thời gian, biểu diễn thành hàm dạng s=vt+s0.
Tương tự, trong kinh tế học, chi phí sản xuất thay đổi theo sản lượng thường biểu thị qua hàm bậc nhất. Ví dụ: C(x)=100x+2000 thể hiện chi phí thay đổi theo số lượng hàng hóa sản xuất.
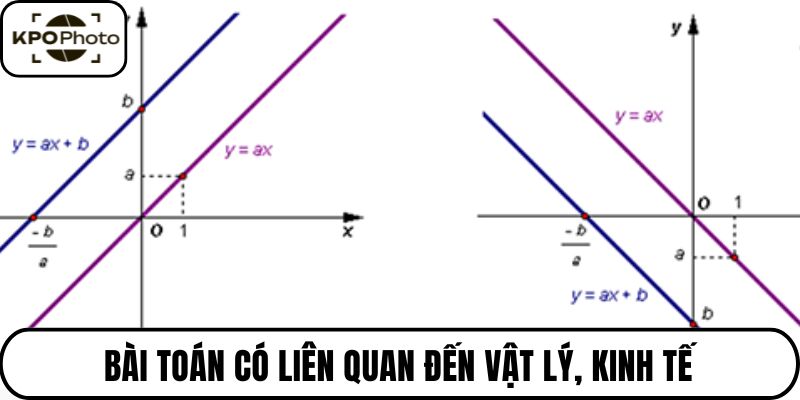
Những ứng dụng trên không chỉ giúp học sinh hiểu rõ bản chất hàm số, mà còn tăng tính kết nối giữa toán học, thực tiễn. Việc gắn lý thuyết vào bối cảnh cụ thể khiến kiến thức trở nên dễ nhớ hơn.
Ngoài ra, các mô hình thống kê cơ bản cũng dùng hàm bậc nhất để ước lượng xu hướng. Do vậy, nắm được dạng này là bước đầu để học tốt môn toán ứng dụng.
Ví dụ thực tiễn dùng hàm số bậc nhất trong đời sống
Một công ty tính lương nhân viên theo công thức cố định kèm thưởng theo sản phẩm có thể dùng hàm y=ax+b. Trong đó, aaa là tiền thưởng cho mỗi sản phẩm, bbb là lương cố định hàng tháng.
Tính toán khoảng cách giữa hai địa điểm khi biết vận tốc, thời gian cũng là một ví dụ tiêu biểu. Đây là tình huống thường gặp khi học sinh làm bài toán chuyển động cơ học trong chương trình phổ thông.
Giá điện, tiền nước được tính theo bậc có thể biểu thị từng phần bằng các đoạn hàm bậc nhất. Việc nắm chắc mô hình này giúp hiểu rõ hóa đơn gia đình và lập kế hoạch tài chính cá nhân.
Ứng dụng rộng rãi của hàm số bậc nhất cho thấy đây không chỉ là kiến thức thi cử. Mà còn là công cụ hữu hiệu để tư duy logic, phân tích các tình huống trong đời sống.
Xem thêm: Hàm Số Bậc Nhất – Kiến Thức Nền Tảng Và Cách Ghi Nhớ
Lỗi sai thường gặp và cách khắc phục
Một trong những nguyên nhân khiến học sinh mất điểm trong bài toán HSBN là do thao tác biến đổi sai phổ biến mà kpophoto sẽ trình bày bên dưới. Ngoài ra, việc chủ quan trong bước kiểm tra kết quả cũng khiến đáp án bị lệch đáng kể.
Sai lầm khi biến đổi phương trình
Nhiều học sinh nhầm lẫn khi chuyển vế hoặc rút gọn biểu thức, nhất là khi có dấu âm hoặc phân số. Việc quên đổi dấu hay gộp nhầm hằng số dễ khiến kết quả sai ngay từ bước đầu.
Khi giải phương trình hoán vị, việc không đưa về cùng một dạng khiến bài toán trở nên phức tạp. Lời khuyên là nên nhóm các biến và hằng số rõ ràng, kiểm soát từng phép toán để tránh mắc lỗi.
Một lỗi phổ biến khác là bỏ qua điều kiện xác định của phương trình, đặc biệt khi có mẫu số hoặc căn thức. Nhiều học sinh vội vàng khử mẫu hoặc bình phương hai vế mà không xét tính hợp lệ của nghiệm, dẫn đến kết quả sai.
Ngoài ra, việc áp dụng máy móc công thức mà không hiểu bản chất khiến bài giải trở nên rườm rà, thiếu chính xác. Để khắc phục, cần rèn thói quen đặt điều kiện trước khi biến đổi, thử lại nghiệm sau khi giải.
Cách kiểm tra kết quả để tránh bẫy đề bài
Một cách hiệu quả để tránh sai sót là thay ngược lại kết quả vào đề bài. Việc này không tốn nhiều thời gian nhưng giúp phát hiện nhanh lỗi sai logic trong quá trình giải.
Ngoài ra, khi có nhiều đáp án gần giống nhau, cần để ý đơn vị, dấu hiệu đặc trưng hoặc điều kiện biên. Một chi tiết nhỏ bị bỏ qua có thể làm lệch toàn bộ kết quả.
Sử dụng bảng biến thiên hoặc đồ thị minh họa cũng là phương pháp kiểm tra chéo hữu ích. Khi kết hợp nhiều cách, khả năng nhận diện lỗi và sửa sai sẽ cải thiện đáng kể.
Kết luận
Hiểu rõ bản chất của hàm số bậc nhất giúp nâng cao nền tảng tư duy toán học. Khi kết hợp kiến thức lý thuyết với tư duy giải nhanh, học sinh có thể xử lý bài tập chính xác và hiệu quả. Kpophoto hy vọng đã cung cấp một góc nhìn đầy đủ, thực tế và chuyên sâu về chủ đề này, từ đó hỗ trợ quá trình học tập và luyện thi đạt kết quả tốt hơn.