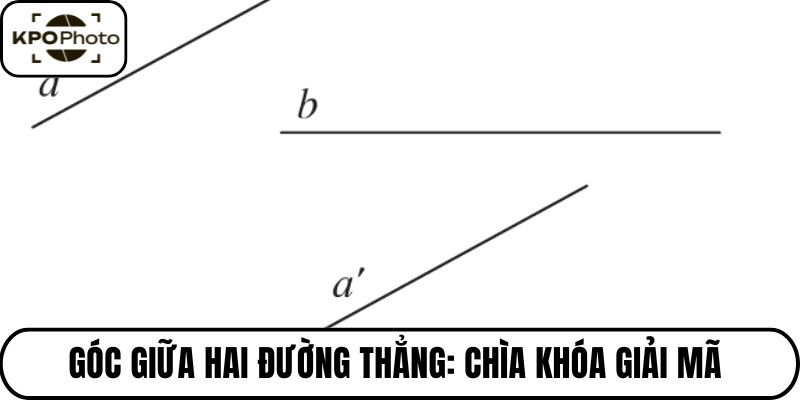
Góc giữa hai đường thẳng khi nghe đến cụm từ này có thể bạn sẽ hình dung ngay đến những công thức toán học có phần khô khan. Nhưng hãy thử nhìn xa hơn, ra thế giới xung quanh bạn. Từ những đường chéo trên một tác phẩm kiến trúc hiện đại, quỹ đạo của một tia laser. Khái niệm này kpophoto thấy hiện diện ở khắp mọi nơi, định hình nên mối quan hệ và sự tương tác trong không gian.
Bản chất thực sự của góc giữa hai đường thẳng là gì?
Trước khi đi sâu vào những con số, chúng ta hãy cùng nhau cảm nhận về bản chất của nó. Về cơ bản, góc giữa hai đường thẳng là một số đo, cho chúng ta biết độ “lệch” hay độ “mở” giữa hai đường thẳng đó.
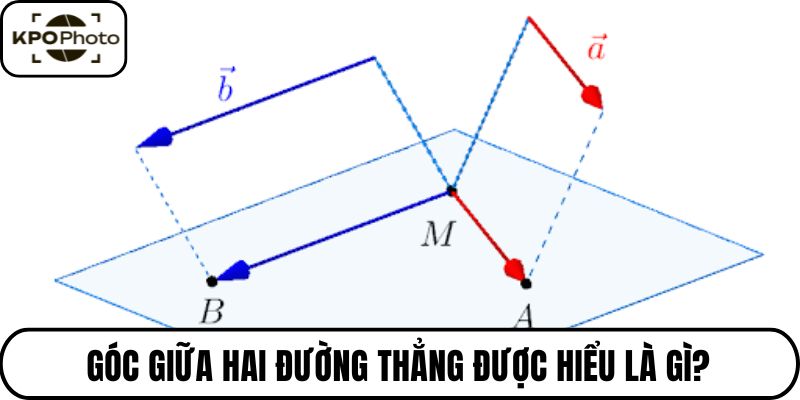
Nó không chỉ là một giá trị trừu tượng. Mà là một câu chuyện kể về cách hai con đường hình học gặp gỡ, song hành hay lướt qua nhau.
Khái niệm trực quan – Khi hai đường thẳng cắt nhau
Đây là trường hợp đơn giản và dễ hình dung nhất. Khi hai đường thẳng cắt nhau trong một mặt phẳng, chúng tạo ra bốn góc. Tuy nhiên, theo quy ước trong toán học góc giữa hai đường thẳng luôn được định nghĩa là góc nhỏ nhất trong số bốn góc đó. Điều này có nghĩa là giá trị của nó sẽ luôn nằm trong khoảng từ 0° đến 90°.
Trường hợp đặc biệt – Song song và trùng nhau
Khi hai đường thẳng song song chúng không bao giờ gặp nhau, luôn giữ một khoảng cách không đổi. Chúng có cùng một phương. Trong trường hợp này, góc giữa hai đường thẳng được quy ước là 0°. Hoặc khi hai đường thẳng trùng nhau thì chúng thực chất là một. Độ lệch giữa chúng không tồn tại. Do đó, góc giữa hai đường cũng là 0°.
Thử thách lớn nhất khi hai đường thẳng chéo nhau
Đây là phần thú vị và cũng là phần khiến nhiều người bối rối nhất. Hai đường thẳng chéo nhau là hai đường thẳng không song song và cũng không cắt nhau (hãy tưởng tượng một cây cầu vượt qua một con đường bên dưới). Vậy làm sao để đo góc giữa hai đường thẳng khi chúng không hề chạm vào nhau? Câu trả lời nằm ở một phương pháp vô cùng thông minh:
- Chọn một điểm O bất kỳ trong không gian (để đơn giản, ta thường chọn một điểm nằm trên một trong hai đường thẳng).
- Từ điểm O đó, ta vẽ hai đường thẳng mới, mỗi đường thẳng song song với một trong hai đường thẳng ban đầu.
- Lúc này, hai đường thẳng mới sẽ cắt nhau tại O. Góc giữa hai đường thẳng ban đầu chính là góc được tạo bởi hai đường thẳng mới này tại O.
Đây là một giải thích rõ nét mang tính đột phá, cho phép chúng ta “mang” phương của hai đường thẳng chéo nhau về chung một gốc để đo lường. Nhờ đó, bài toán xác định góc trong không gian trở nên khả thi.
Công cụ toán học – Công thức chính xác để tìm
Cảm nhận và hình dung là bước đầu tiên, nhưng để có được sự chính xác tuyệt đối, chúng ta cần đến những công cụ toán học mạnh mẽ. Sức mạnh này nằm gọn trong khái niệm vector.
Trong mặt phẳng Oxy – Sức mạnh của Vector chỉ phương
Trong hệ tọa độ Oxy, mỗi đường thẳng đều có một hoặc vô số vector chỉ phương (vector có giá song song hoặc trùng với đường thẳng). Giả sử đường thẳng d₁ có vector chỉ phương u1=(a1;b1) và d₂ có vector chỉ phương u2⃗=(a2;b2)u2=(a2;b2). Khi đó, công thức tính góc giữa hai đường thẳng được xác định thông qua cosin của góc φ giữa chúng:

Giải thích chi tiết: Dấu giá trị tuyệt đối ở trên tử số (|…|) là cực kỳ quan trọng. Nó đảm bảo rằng giá trị cos luôn dương, từ đó góc φ tính ra sẽ luôn là góc nhọn (từ 0° đến 90°). Hoàn toàn phù hợp với định nghĩa về góc giữa hai đường thẳng mà chúng ta đã nói ở trên.
Trong không gian Oxyz – Vẫn là câu chuyện của Vector
Điều tuyệt vời là logic này vẫn được áp dụng một cách hoàn hảo cho không gian ba chiều. Sự khác biệt duy nhất là vector chỉ phương bây giờ có thêm thành phần thứ ba (cao độ z). Nếu d₁ có vector chỉ phương:
u1⃗=(a1;b1;c1)u1=(a1;b1;c1) và d₂ có u2⃗=(a2;b2;c2)u2=(a2;b2;c2), công thức tính góc giữa hai đường thẳng gần như không thay đổi:
Công thức này chính là công cụ vạn năng, giúp bạn tìm ra góc giữa hai đường bất kể chúng cắt nhau hay chéo nhau trong không gian. Miễn là bạn xác định được vector chỉ phương của chúng.
Xem thêm: Công Thức Hình Chóp – Bật Mí Vẻ Đẹp Học Thuật Và Kiến Trúc
Góc giữa hai đường thẳng trong cuộc sống
toán học chỉ thực sự ý nghĩa khi nó có thể được áp dụng. Và khái niệm là một minh chứng sống động cho điều đó.
Kiến trúc, xây dựng và thiết kế
Hãy nhìn vào mái của một ngôi nhà. Độ dốc của mái, yếu tố quyết định khả năng thoát nước và thẩm mỹ của công trình, chính là góc giữa hai đường thẳng: một đường trên mái và một đường ngang (mặt phẳng). Các kiến trúc sư phải tính toán góc này một cách cẩn thận.

Trong thiết kế nội thất, việc đặt một chiếc ghế sofa chéo góc hay một chiếc kệ sách không song song với tường.Từ đây sẽ tạo ra những góc khác nhau, ảnh hưởng trực tiếp đến cảm nhận không gian và luồng di chuyển trong phòng.
Góc giữa hai đường thẳng cùng kỹ thuật cơ khí & robot
Trong một động cơ, các piston và trục khuỷu di chuyển theo những góc độ được tính toán chính xác. Cánh tay của một con robot công nghiệp có thể gắp một vật thể một cách chuẩn xác là nhờ vào việc kiểm soát hoàn hảo góc giữa hai đường thẳng tạo bởi các khớp nối của nó.
Một giải thích rõ nét hơn là: mỗi khớp quay đều thay đổi góc giữa hai bộ phận, và bộ điều khiển trung tâm phải tính toán hàng nghìn phép tính góc mỗi giây. Nhằm để tạo ra chuyển động mượt mà.
Lập trình đồ họa, game và thực tế ảo
Đây là một lĩnh vực mà góc giữa hai đường thẳng thực sự tỏa sáng.
- Phát hiện va chạm: Làm sao game biết được viên đạn của bạn đã trúng tường? Nó tính toán quỹ đạo của viên đạn (một đường thẳng) và kiểm tra xem nó có cắt các đường thẳng tạo nên bề mặt của bức tường không.
- Hiệu ứng ánh sáng: Sự phản xạ của ánh sáng trên một mặt nước lung linh được lập trình dựa trên nguyên tắc vật lý cơ bản: góc tới bằng góc phản xạ. Cả hai góc này đều được xác định dựa trên góc giữa hai đường thẳng: tia sáng tới (hoặc tia phản xạ) và đường pháp tuyến của bề mặt.

- Tầm nhìn của AI: Một nhân vật kẻ địch trong game có một “vùng nhìn” hình nón. Vùng nhìn này được xác định bởi một góc. Nếu đường thẳng từ kẻ địch tới người chơi nằm trong góc đó, bạn sẽ bị phát hiện.
Lĩnh vực hàng không và hàng hải
Khi một con tàu chuyển hướng hay một chiếc máy bay đổi lộ trình, phi công và thuyền trưởng phải tính toán góc chuyển hướng một cách chính xác. Góc này chính là góc giữa hai đường thẳng: đường đi hiện tại và đường đi mong muốn. Sai một độ cũng có thể dẫn đến lệch hàng chục, hàng trăm cây số sau một hành trình dài.
Lời kết
Góc giữa hai đường thẳng không chỉ là một phép đo trong hình học. Theo kpophoto thì đây là ngôn ngữ của sự định hướng, của mối quan hệ của sự tương tác. Từ những cấu trúc vĩ đại nhất do con người tạo ra cho đến những thế giới ảo đầy mê hoặc. Nó luôn ở đó, âm thầm nhưng mạnh mẽ kết nối thế giới trừu tượng của toán học với thực tại sống động quanh ta.