Góc giữa hai đường thẳng là đại lượng đo lường mức độ lệch giữa hai phương trong không gian ba chiều, đóng vai trò then chốt trong các bài toán vector, mặt phẳng. Đây là khái niệm xuất hiện phổ biến trong hình học giải tích và được ứng dụng trong nhiều lĩnh vực như cơ học, kiến trúc, đồ họa máy tính. Toàn bộ nội dung đã được kiểm định bởi bộ phận chuyên môn tại kpophoto nhằm đảm bảo độ chính xác cao nhất.
Định nghĩa cơ bản góc giữa hai đường thẳng trong không gian
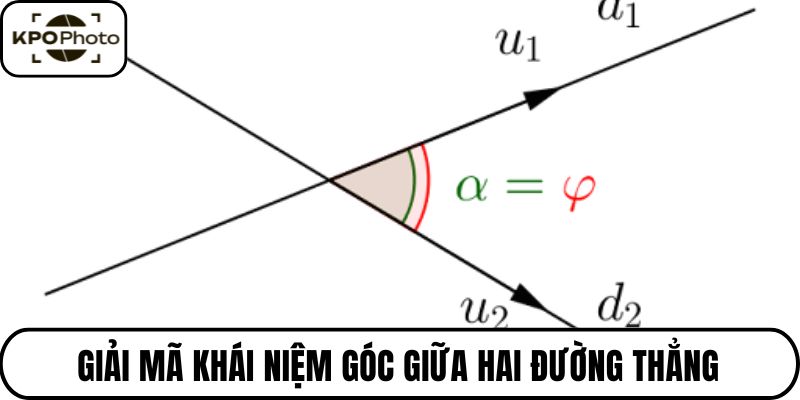
Góc giữa hai đường thẳng được định nghĩa là góc nhỏ nhất tạo bởi hai đường thẳng cắt nhau hoặc hai đường thẳng chéo nhau. Trong hình học không gian, định nghĩa này giữ vai trò đặc biệt trong việc thiết lập quan hệ giữa các phần tử cơ bản của hình khối. Một cách chính xác, đó là góc nhọn (nhỏ hơn hoặc bằng 90 độ) được tạo bởi hai vectơ chỉ phương của hai đường thẳng cần xét.
Đối với hai đường thẳng cắt nhau, ta có thể xác định góc giữa chúng bằng cách dùng tích vô hướng của hai vectơ chỉ phương. Nếu hai đường thẳng chéo nhau (không đồng phẳng, không cắt), phương pháp tương tự vẫn được áp dụng. Tất cả được thể hiện thông qua vectơ đại diện và tính toán trong hệ tọa độ ba chiều.
Đây là khái niệm phổ biến trong chương trình toán học phổ thông và thường áp dụng trong bài thi có độ khó cao ở cấp độ học sinh trung học phổ thông. Việc hiểu sâu lý thuyết này giúp thí sinh xử lý nhanh các bài toán không gian. Đặc biệt trong các kỳ thi tuyển sinh đại học hoặc kỳ thi chọn học sinh giỏi.
Tính góc giữa hai đường thẳng từ công thức đã cho
Góc giữa hai đường thẳng được xác định thông qua tích vô hướng của hai vector chỉ phương tương ứng. Để giải chính xác các bài toán liên quan, người học cần nắm vững công thức tính cùng điều kiện áp dụng.
Trường hợp cho hai đường thẳng cắt nhau
Giả sử ta có hai vectơ chỉ phương u và v của hai đường thẳng d1 và d2, khi đó:
cos(θ)=|u·v|/(||u|| × ||v||).
Với θ\thetaθ là góc giữa hai đường thẳng, biểu thức này cho thấy việc tính toán dựa vào tích vô hướng giữa hai vectơ, sau đó lấy trị tuyệt đối để đảm bảo luôn thu được giá trị không âm. Kết quả này giúp ta tìm ra góc nhọn, ngay cả khi hai vectơ lệch chiều.
Trường hợp cho hai đường thẳng chạy song song
Nếu hai đường thẳng song song, thì góc giữa chúng sẽ bằng 0 độ nếu cùng hướng hoặc 180 độ nếu ngược hướng. Trong hình học không gian, ta chỉ xét đến góc nhọn hoặc góc tù nhỏ hơn hoặc bằng 90 độ, nên với song song, góc thường tính là 0 độ.
Trường hợp cho hai đường thẳng chỉ chéo nhau
Khi hai đường không cắt nhau và không song song (tức là chéo nhau), ta cần chọn hai vectơ chỉ phương của chúng và đưa về cùng hệ tọa độ. Sau đó, vẫn áp dụng công thức trên để tính góc giữa chúng như trường hợp cắt nhau. Phép tính lúc này cần lưu ý thêm bước dựng vectơ, chọn điểm mốc và đảm bảo không sai lệch do góc không nằm trong cùng mặt phẳng.
Ứng dụng trong hình học không gian thực tế
Trong thực tiễn, việc xác định góc giữa hai đường thẳng không chỉ dừng lại ở bài toán lý thuyết. Đây còn là công cụ phân tích cấu trúc hình học của vật thể trong kiến trúc, thiết kế 3D, kỹ thuật cơ khí và nhiều lĩnh vực kỹ thuật khác. Khi lập mô hình 3D, các phần mềm CAD thường yêu cầu tính toán chính xác góc giữa các cạnh hoặc trục để đảm bảo tính đúng đắn về kết cấu.
Ví dụ, trong xây dựng kết cấu thép, việc xác định góc giữa các thanh giằng là cực kỳ quan trọng. Sai lệch dù chỉ 1 độ có thể ảnh hưởng tới sự phân bố lực và tính ổn định của toàn bộ công trình. Tương tự, trong công nghệ robot, việc thiết kế khớp nối giữa hai thanh tay máy yêu cầu tính góc giữa chúng chính xác để đảm bảo sự phối hợp chuyển động mượt mà.
Đáng chú ý, ngành hàng không cũng ứng dụng lý thuyết này để tính toán góc bay giữa các tuyến đường bay trong không gian ba chiều. Từ đó giúp thiết kế lộ trình tối ưu cho máy bay dân dụng cũng như quân sự. Ngoài ra nó còn giúp đảm bảo an toàn bay, hạn chế va chạm và nâng cao hiệu suất vận hành của hệ thống điều hướng hàng không.
Phân tích góc giữa hai đường thẳng qua ví dụ thực tế
Góc giữa hai đường thẳng không chỉ là khái niệm hình học trừu tượng mà còn xuất hiện trong nhiều tình huống thực tế quen thuộc. Việc phân tích các ví dụ cụ thể giúp làm rõ bản chất không gian và ứng dụng hiệu quả trong tính toán.
Ví dụ trong mặt phẳng tọa độ
Cho hai đường thẳng d1 và d2 với phương trình tổng quát:
d₁: y = 2x + 1
d₂: y = −½x +
Hệ số góc của d₁ là m₁ = 2, của d₂ là m₂ = −½. Khi đó, hãy áp dụng công thức tính góc giữa hai đường thẳng như sau:
tan(θ)=|(m₂ – m₁)/(1 + m₁·m₂)|.
Mẫu số bằng 0 nên ta suy ra hai đường này vuông góc. Như vậy, góc giữa hai đường thẳng bằng 90 độ. Đây là trường hợp đặc biệt quan trọng thường gặp trong các bài toán chứng minh tính vuông góc giữa hai vector chỉ phương.
Ví dụ góc giữa hai đường thẳng trong không gian ba chiều
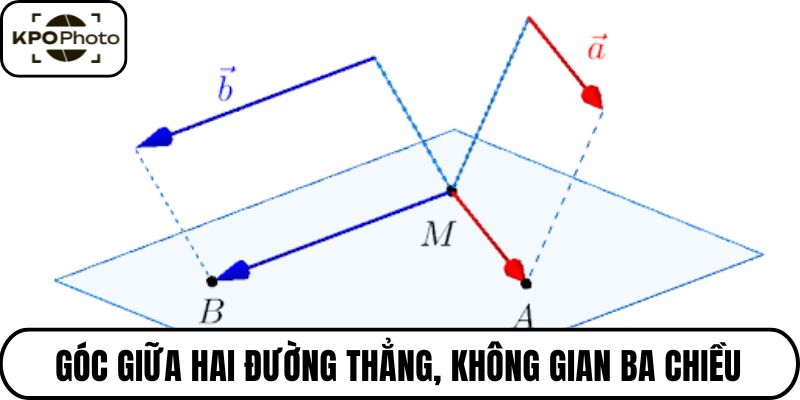
Giả sử cho hai đường thẳng có các vectơ chỉ phương tương ứng được xác định như dưới đây:
- u = (1, 2, 3)
- v = (4, 5, 6)
Tích vô hướng:
u.v = 1×4 + 2×5 + 3×6 = 4 + 10 + 18 = 32
Tính độ dài của từng vectơ:
- Độ dài u = √(1² + 2² + 3²) = √14
- Độ dài v = √(4² + 5² + 6²) = √77
Áp dụng công thức tính cosine góc giữa hai vectơ:
cos(θ)=∥u∥⋅∥v∥u⋅v=14⋅7732≈0.9746
Vậy: θ≈cos−1(0.9746)≈12.9∘
Qua ví dụ được kpophoto đưa ra, ta thấy góc giữa hai đường thẳng trong không gian ba chiều có thể được xác định chính xác bằng công thức lượng giác khi có vectơ chỉ phương rõ ràng. Tuy nhiên, cần lưu ý xác định đúng hướng của các vector để tránh sai lệch về giá trị góc. Việc sử dụng công thức cosin không chỉ cho kết quả chính xác mà còn giúp kiểm tra được mối quan hệ tương đối giữa hai đường trong không gian.
Ví dụ với đường chéo trong hình hộp chữ nhật
Giả sử cần xác định góc giữa hai đường thẳng là hai đường chéo trong một hình hộp chữ nhật nối hai đỉnh không kề nhau, bước đầu tiên là xác định tọa độ các điểm liên quan. Tiếp theo, ta lập các vectơ chỉ phương tương ứng với hai đường chéo đã chọn. Cuối cùng, áp dụng công thức tích vô hướng để tính góc giữa hai vectơ, từ đó suy ra góc giữa hai đường thẳng.
Xem thêm: Định Lý Pitago – Từ Nền Tảng Học Thuật Đến Thực Tiễn Thực Tế
Cách xử lý bài toán phức tạp liên quan đến góc giữa hai đường thẳng
Đối với các đề toán nâng cao, đôi khi góc giữa hai đường thẳng không được cho rõ ràng. Khi đó, người giải cần phân tích hình học không gian kỹ lưỡng, dựa vào giả thiết để dựng các đường phụ hoặc sử dụng các phép chiếu vuông góc. Trong một số trường hợp, phương pháp tọa độ hóa toàn bộ hệ thống không gian là lựa chọn khả thi nhất để chuyển bài toán về dạng đại số thuần túy.

Chẳng hạn, khi cần xác định góc giữa trục xi-lanh, dây chéo căng qua hai cạnh của một hình lập phương, người làm toán phải quy chiếu toàn bộ hệ lên hệ trục tọa độ Oxyz, dựng các vectơ tương ứng. Việc thành thạo trong việc chuyển đổi giữa hình học trực quan, hình học tọa độ giúp quá trình này chính xác hơn, đặc biệt trong các bài yêu cầu chứng minh tính chất không gian.
Kết luận
Góc giữa hai đường thẳng là kiến thức cốt lõi trong hình học không gian, đóng vai trò cầu nối giữa hình học trực quan, đại số tọa độ. Từ định nghĩa cơ bản đến ứng dụng nâng cao, người học cần nắm chắc quy trình dựng vectơ, tính tích vô hướng, xác định đúng góc cần tìm. Bài viết do đội ngũ biên tập kỹ thuật của kpophoto kiểm định, đảm bảo độ chính xác, tính ứng dụng trong nhiều lĩnh vực học thuật lẫn thực tiễn.

