Định lý Pitago là một trong những nguyên lý toán học nền tảng trong chương trình hình học phẳng và không gian. Không chỉ xuất hiện thường xuyên trong bài học, công thức này còn có vai trò chủ đạo trong nhiều bài toán thực tiễn. Nội dung bài viết do đội ngũ chuyên môn tại kpophoto tổng hợp và xác minh dựa trên kiến thức đã được chuẩn hóa.
Định lý Pitago và cách phát biểu chuẩn xác
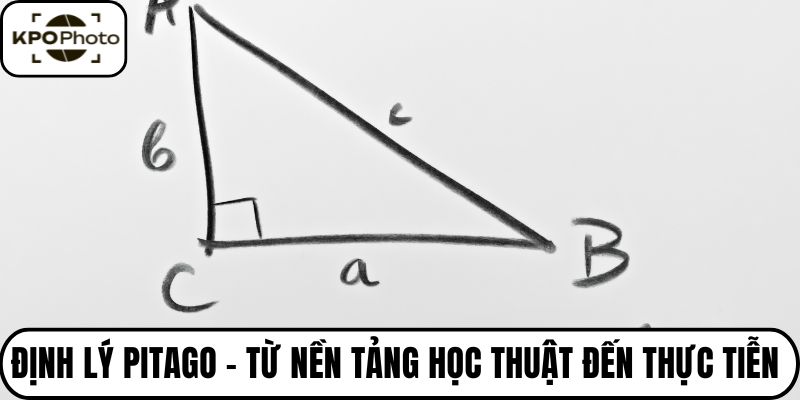
Định lý Pitago mô tả mối quan hệ giữa ba cạnh trong tam giác vuông, vốn là dạng hình cơ bản nhất trong hình học. Phát biểu cụ thể: Trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông. Công thức chuẩn là:
c² = a² + b², trong đó c là cạnh huyền, a và b là hai cạnh góc vuông.
Không chỉ đơn thuần là một công thức, định lý Pitago còn là cơ sở để xây dựng các quy tắc tính toán phức tạp hơn như công thức tọa độ, hệ thức lượng, hoặc khi phân tích các đại lượng hình học trong không gian ba chiều.

Định lý này có nguồn gốc từ toán học Hy Lạp cổ đại, gắn liền với tên tuổi nhà toán học Pythagoras, nhưng thực tế đã được các nền văn minh như Babylon và Ai Cập sử dụng từ trước đó. Việc chứng minh định lý đã được thực hiện bằng nhiều cách khác nhau, từ hình học thuần túy đến đại số. Đặc biệt, trong giáo dục hiện đại, định lý này đóng vai trò mở đầu cho việc phát triển tư duy logic và kỹ năng suy luận hình học.
Ứng dụng định lý Pitago trong hình học phẳng
Định lý Pitago là công cụ nền tảng khi giải quyết các bài toán liên quan đến khoảng cách, độ dài trong mặt phẳng tọa độ. Trong hình học phẳng, định lý này thường xuất hiện khi cần chứng minh tam giác vuông hoặc tính cạnh chưa biết.
Tính khoảng cách giữa hai điểm
Giả sử trong mặt phẳng tọa độ Oxy, cần tính khoảng cách từ điểm A(x₁, y₁) đến điểm B(x₂, y₂), ta sử dụng công thức rút ra từ định lý Pitago:
Ta có: AB = √[(x₂ – x₁)² + (y₂ – y₁)²]
Công thức này thể hiện rõ cách tạo tam giác vuông bằng trục hoành và trục tung, với hai cạnh góc vuông lần lượt là hiệu hoành độ và tung độ của hai điểm. Việc sử dụng tổng bình phương hai cạnh góc vuông cho phép xác định cạnh huyền một cách chính xác. Đây chính là khoảng cách từ A đến B trong mặt phẳng hai chiều.
Xác định tính vuông của một tam giác
Cho ba điểm bất kỳ trên mặt phẳng, có thể xác định tam giác tạo thành có vuông hay không bằng cách so sánh bình phương độ dài ba cạnh. Nếu đúng a² + b² = c², tức tam giác vuông tại đỉnh đối diện cạnh huyền. Đây là phương pháp thường gặp khi áp dụng trong bài thi liên quan đến tọa độ hoặc hình học phẳng.

Theo kpophoto, phương pháp này đặc biệt hữu ích trong các bài toán chứng minh hình dạng hình học. Chẳng hạn kiểm tra xem một tứ giác có là hình chữ nhật hay không thông qua các tam giác con. Khi làm việc với hệ trục tọa độ, ta thường tính độ dài cạnh bằng công thức căn bậc hai rồi bình phương để so sánh trực tiếp.
Ứng dụng đối với hình tam giác đặc biệt
Tam giác vuông cân, tam giác 30-60-90, hoặc tam giác 45-45-90 đều có thể được giải quyết dễ dàng bằng định lý Pitago. Trong mỗi trường hợp, cạnh huyền sẽ mang giá trị cố định so với cạnh góc vuông. Nhờ đó giảm thời gian tính toán trong các bài tập trắc nghiệm.
Phân tích định lý Pitago qua ví dụ thực tế
Định lý Pitago không chỉ tồn tại trên sách vở mà còn hiện diện trong nhiều tình huống thực tế, đặc biệt trong các phép đo khoảng cách. Việc vận dụng đúng định lý này giúp giải quyết hiệu quả các bài toán hình học gắn liền với đời sống, kỹ thuật.
Trong thiết kế kiến trúc
Kỹ sư xây dựng thường sử dụng định lý Pitago để xác định chiều dài đường chéo trong bản vẽ nhà, cầu thang hoặc trụ đỡ. Ví dụ điển hình là khi cần tính toán chiều cao cần thiết của cầu thang dựa trên chiều dài mặt, độ cao tầng đã biết. Khi đó, công thức c² = a² + b² cho phép nhanh chóng xác định độ dài đoạn xiên một cách chính xác, đáng tin cậy.
Trong bản đồ học, định vị GPS
Trong bản đồ học, hệ thống định vị GPS, định lý Pitago được sử dụng để tính khoảng cách giữa hai điểm có tọa độ xác định. Khi biết tọa độ của hai điểm trên mặt phẳng hoặc không gian, có thể áp dụng trực tiếp công thức khoảng cách rút ra từ định lý này. Công nghệ GPS hiện đại tính toán khoảng cách từ thiết bị đến vệ tinh dựa trên nguyên lý tam giác vuông để định vị chính xác vị trí.
Trong vật lý cơ bản
Nếu vật thể di chuyển theo hai phương vuông góc, quãng đường thực tế di chuyển chính là cạnh huyền của tam giác tạo bởi hai phương chuyển động. Khi ấy, quãng đường được tính bằng công thức tổng bình phương quãng đường trên từng phương. Đây là cách vận dụng định lý Pitago để đo vận tốc tổng hợp hoặc quãng đường thực tế.

Ngoài việc tính quãng đường, định lý Pitago còn được dùng để xác định độ lớn của lực tổng hợp khi hai lực tác động vuông góc lên một vật thể. Trường hợp điển hình là khi một vật chịu đồng thời lực kéo ngang, trọng lực thẳng đứng, lực hợp sẽ là cạnh huyền của tam giác lực. Cách tính này không chỉ chính xác mà còn tiết kiệm thời gian trong việc giải bài tập cơ học cổ điển.
Xem thêm: Tọa Độ Trong Không Gian – Chìa Khóa Mở Ra Thế Giới Ba Chiều
Tổng hợp các dạng bài thường gặp liên quan đến định lý Pitago
Các bài toán liên quan đến định lý Pitago thường xuất hiện với nhiều hình thức đa dạng từ cơ bản đến nâng cao. Học sinh cần phân biệt rõ từng kiểu bài để lựa chọn cách tiếp cận phù hợp trong từng trường hợp cụ thể.
Tính độ dài các cạnh ở trong một hình tam giác vuông
Dạng toán này yêu cầu vận dụng trực tiếp công thức để tính cạnh còn lại trong tam giác vuông. Thí sinh chỉ cần thay số vào công thức c²= a² + b², rút gọn. Đây là dạng bài đơn giản nhất nhưng có vai trò nền tảng cho những bài nâng cao hơn.
Tìm tọa độ điểm thỏa mãn điều kiện trong hình học
Dạng bài này thường xuất hiện trong chương trình nâng cao, đòi hỏi kỹ năng phối hợp giữa hình học giải tích, đại số. Cụ thể, điểm M cần được xác định sao cho tam giác AMB là tam giác vuông tại M hoặc một đỉnh khác. Khi đó, định lý Pitago giúp thiết lập các phương trình liên quan đến khoảng cách giữa các điểm để tìm tọa độ thỏa mãn.

Khi giải bài toán kiểu này, người học thường sử dụng công thức khoảng cách để biểu diễn độ dài các cạnh của tam giác theo tọa độ điểm chưa biết. Sau đó, áp dụng công thức để tạo phương trình giữa ba cạnh, từ đó giải ra hoành độ và tung độ của điểm M. Đây là một trong những ứng dụng điển hình cho thấy sự kết nối giữa hình học thuần túy và đại số trong việc xử lý các bài toán tọa độ phức tạp.
Chứng minh tam giác vuông
Dựa trên độ dài ba cạnh, ta kiểm tra điều kiện bằng công thức a² + b² = c², trong đó c là cạnh dài nhất. Nếu đẳng thức này đúng, có thể kết luận tam giác là vuông theo định lý Pitago. Dạng toán này thường xuất hiện trong chứng minh tính chất hình học hoặc nhận dạng tam giác từ dữ liệu tọa độ.
Kết luận
Định lý Pitago là nền tảng toán học được sử dụng rộng rãi trong nhiều lĩnh vực học thuật và thực tiễn. Bằng cách áp dụng đúng cách, công thức này mang lại độ chính xác cao trong các phép đo và phân tích hình học. Những nội dung trong bài viết đã được xác thực bởi đội ngũ chuyên môn từ kpophoto, đảm bảo tính toàn vẹn và tin cậy.