Công thức logarit là một công cụ toán học mang tính cách mạng, cho phép chúng ta biến đổi những phép tính phức tạp thành những phép tính đơn giản hơn. Nó là ngôn ngữ của sự tăng trưởng theo cấp số nhân và phân rã. Kpophoto sẽ giúp bạn khám phá tổng quan cũng như ứng dụng của chúng nhiều lĩnh vực.
Tổng quan về công thức logarit
Logarit, một trong những khái niệm nền tảng của toán học, là công cụ không thể thiếu trong nhiều lĩnh vực khoa học và kỹ thuật. Hiểu rõ về chúng tại Kpophoto sẽ mở ra cánh cửa đến việc giải quyết các bài toán phức tạp.
Logarit là gì?
Logarit là phép toán ngược của lũy thừa. Chúng trả lời cho câu hỏi một số cơ sở phải được nâng lên lũy thừa bao nhiêu để có được một giá trị cụ thể. Chẳng hạn, nếu 102=100, thì logarit cơ số 10 của 100 là 2.

Mối quan hệ giữa công thức logarit và hàm số mũ rất chặt chẽ. Cụ thể, logb(x)=y tương đương với by=x. Trong đó, b là cơ số, x là đối số, và y là giá trị logarit. Việc nắm vững mối liên hệ này sẽ giúp bạn dễ dàng chuyển đổi giữa hai dạng biểu thức.
Ký hiệu và cách đọc công thức logarit
Có ba loại ký hiệu trong logarit phổ biến mà bạn cần biết. Thứ nhất là logb(x), được đọc là “logarit cơ số b của x”. Thứ hai là ln(x), ký hiệu cho logarit tự nhiên, với cơ số là hằng số e (khoảng 2.718). Cuối cùng là log(x), thường dùng cho logarit thập phân, với cơ số 10, nếu không được ghi rõ.
Điều kiện xác định của logarit
Đầu tiên, cơ số b phải là một số dương và khác 1 (b>0,b=1). Nếu cơ số bằng 1, biểu thức sẽ không xác định. Thứ hai, đối số x luôn phải là một số dương (x>0). Điều kiện này đảm bảo rằng giá trị logarit là số thực. Việc bỏ qua những quy tắc này có thể dẫn đến các kết quả sai hoặc không hợp lệ.
Tổng hợp các quy tắc công thức logarit cơ bản
Sau khi đã hiểu rõ về định nghĩa và các điều kiện xác định, chúng ta sẽ đi vào những quy tắc biến đổi cơ bản. Đây là nền tảng để bạn có thể giải quyết hầu hết các bài toán liên quan.
Phép tính logarit của một tích
Khi tính logarit của một tích, chúng ta có thể chuyển nó thành tổng của các logarit riêng lẻ. Quy tắc này được biểu diễn bằng công thức logb(xy)=logb(x)+logb(y). Điều này có nghĩa là công thức logarit của tích hai số bằng tổng logarit của từng số.
Ví dụ, log2(8×4)=log2(8)+log2(4)=3+2=5. Quy tắc này rất hữu ích khi bạn cần tách một biểu thức phức tạp thành các phần nhỏ hơn. Bạn sẽ thấy nó áp dụng trong bài thi rất nhiều.
Phép tính logarit của một thương
Tương tự như tích, logarit của một thương có thể được biến đổi thành hiệu của các logarit. Công thức là logb(x/y)=logb(x)−logb(y). Đây là quy tắc cho phép bạn chia tách các công thức logarit phức tạp.
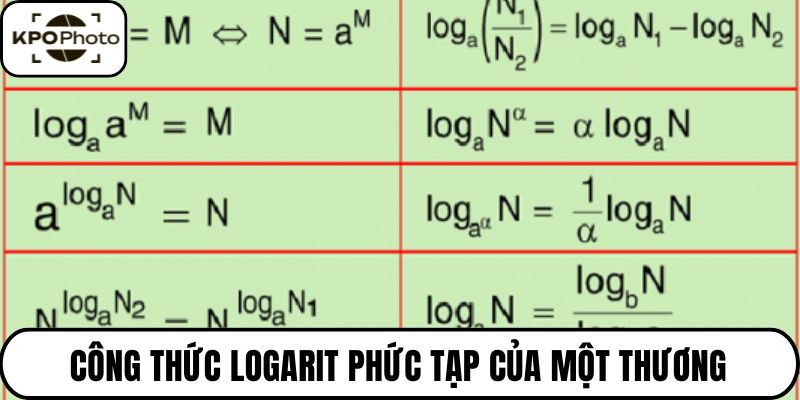
Chẳng hạn, log3(81/9)=log3(81)−log3(9)=4−2=2. Việc áp dụng đúng quy tắc này giúp đơn giản hóa đáng kể quá trình tính toán. Nó là một công cụ mạnh mẽ trong giải các phương trình.
Phép tính logarit của một lũy thừa
Logarit của một lũy thừa cho phép bạn đưa số mũ ra ngoài logarit. Quy tắc này được viết là logb(xn)=n⋅logb(x). Đây là một trong những công cụ mạnh nhất để biến đổi các công thức logarit.
Ví dụ, log5(253)=3⋅log5(25)=3⋅2=6. Sử dụng quy tắc này giúp giảm độ phức tạp của bài toán. Nó đặc biệt hữu ích khi xử lý các phương trình mũ.
Phép tính logarit chuyển cơ số
Quy tắc chuyển cơ số là cực kỳ quan trọng khi bạn cần tính logarit mà máy tính hoặc máy tính không hỗ trợ cơ số đó. Công thức là logb(x)=logk(b)logk(x). Trong đó, k là một cơ số mới mà bạn chọn, thường là 10 hoặc e.
Ví dụ, để tính log2(7), bạn có thể chuyển sang công thức logarit tự nhiên: ln(2)ln(7). Quy tắc này mở rộng khả năng tính toán của bạn. Nó cho phép làm việc linh hoạt với nhiều hệ cơ số khác nhau.
Các phép tính logarit đặc biệt
Ngoài các quy tắc biến đổi chính, có một số trường hợp đặc biệt mà bạn cần ghi nhớ. Đầu tiên là logb(1)=0. Điều này có nghĩa là bất kỳ số nào (trừ 1) mũ 0 đều bằng 1. Đây là một quy tắc cơ bản cần nhớ.
Tiếp theo là logb(b)=1. Điều này đơn giản là b1=b. Một quy tắc khác là logb(bn)=n. Cuối cùng, blogb(x)=x, đây là định nghĩa trực tiếp của công thức logarit như một phép toán ngược. Việc nắm vững những trường hợp này sẽ giúp bạn giải quyết bài tập nhanh hơn.
Công thức logarit nâng cao và các biến thể
Sau khi đã làm quen với các quy tắc cơ bản, chúng ta sẽ khám phá những khái niệm phức tạp hơn. Những phép tính này đòi hỏi sự hiểu biết sâu sắc hơn và có nhiều ứng dụng trong các lĩnh vực chuyên môn.
Đạo hàm của hàm logarit
Đạo hàm của hàm logarit là một khái niệm quan trọng trong giải tích. Nó giúp chúng ta tìm ra tốc độ thay đổi tức thời của một hàm logarit. Đạo hàm của hàm ln(x) là x1. Đối với hàm logb(x), đạo hàm của nó là xln(b)1.

Kiến thức này rất hữu ích trong việc phân tích các hàm tăng trưởng hoặc suy giảm. Ví dụ, trong kinh tế, đạo hàm của hàm logarit có thể giúp tính toán tốc độ tăng trưởng của doanh thu.
Tích phân của hàm logarit
Bên cạnh đạo hàm, tích phân của hàm logarit cũng là một phần không thể thiếu. Tích phân là phép toán ngược của đạo hàm. Nó giúp chúng ta tính toán diện tích dưới đường cong của một hàm logarit.
Tích phân của ln(x) là xln(x)−x+C. Việc áp dụng phép tính này đòi hỏi kỹ thuật tích phân từng phần. Sự hiểu biết về tích phân giúp giải quyết các bài toán về tổng lũy kế.
Bất đẳng thức logarit
Bất đẳng thức logarit liên quan đến việc so sánh giá trị giữa các công thức logarit. Ví dụ, nếu b>1, thì logb(x)>logb(y) khi và chỉ khi x>y. Ngược lại, nếu 0<b<1, thì logb(x)>logb(y) khi và chỉ khi x<y. Các bất đẳng thức này rất quan trọng trong việc chứng minh toán học và giải các bài toán tối ưu.
Logarit phức
Trong lĩnh vực số phức, khái niệm logarit được mở rộng thành logarit phức. Không giống như logarit thực chỉ xác định cho số dương, logarit phức có thể xác định cho số phức bất kỳ (trừ 0). Hàm logarit phức là đa trị, có vô số nghiệm. Điều này tạo ra một chiều kích mới cho việc nghiên cứu công thức logarit.
Công thức bất đẳng thức logarit số phức
Xem thêm: Công Thức Logarit: Khám Phá Từ Lý Thuyết Đến Thực Tiễn
Ứng dụng thực tế của phép tính logarit trong đời sống và khoa học
Các công thức logarit không chỉ tồn tại trong sách vở mà còn có vô vàn ứng dụng thực tiễn. Từ các ngành khoa học cơ bản đến công nghệ hiện đại, vai trò của chúng là không thể phủ nhận.
Trong toán học
Trong toán học, phép tính logarit là công cụ mạnh mẽ để giải các phương trình mũ và logarit. Chúng giúp đơn giản hóa các biểu thức phức tạp, biến đổi phép nhân thành phép cộng và phép chia thành phép trừ.
Trong công nghệ thông tin
Trong lĩnh vực này, logarit đóng vai trò cực kỳ quan trọng. Chúng được sử dụng để phân tích độ phức tạp của thuật toán, đặc biệt là trong ký hiệu Big O notation. Ví dụ, thuật toán tìm kiếm nhị phân có độ phức tạp O(logn), cho thấy hiệu suất cao khi xử lý dữ liệu lớn.
Kết luận
Công thức Logarit không chỉ là một chương trong sách giáo khoa, mà là một công cụ phân tích cực kỳ mạnh mẽ. Khả năng biến đổi phép nhân thành phép cộng, lũy thừa thành phép nhân của chúng đã làm thay đổi cách tiếp cận dữ liệu. Nắm vững kiến thức này tại kpophoto sẽ trang bị cho bạn một lợi thế đáng kể trong việc giải quyết các bài toán khó.

