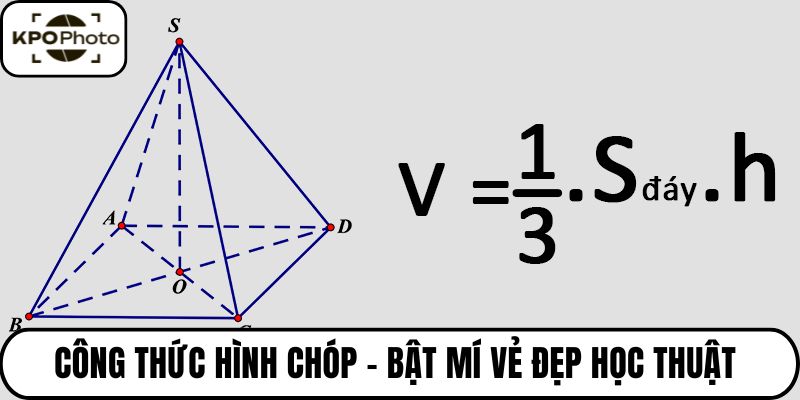
Công thức hình chóp là một trong những cụm từ toán học gợi lên nhiều hình ảnh hùng vĩ nhất trong tâm trí chúng ta. Từ những kim tự tháp Giza sừng sững thách thức thời gian, đến đỉnh kim tự tháp bằng kính của bảo tàng Louvre hiện đại. Từ góc nhìn của kpophoto cho thấy hình chóp luôn là biểu tượng của sự vững chãi, bí ẩn và vẻ đẹp kiến trúc hoàn hảo.
Thấu hiểu linh hồn của hình chóp
Để có thể áp dụng thành thạo bất kỳ công thức hình chóp nào, điều đầu tiên và quan trọng nhất là chúng ta phải thực sự “cảm” được nó. Hình chóp không chỉ là một khối đa diện trong sách giáo khoa. Nó là một cấu trúc có linh hồn được tạo nên từ những yếu tố vô cùng đơn giản nhưng lại kết hợp với nhau một cách hài hòa.
Cấu trúc nền tảng – Đỉnh, đáy và những mặt bên
Hãy cùng nhau mổ xẻ một hình chóp bất kỳ. Bạn sẽ thấy nó được cấu thành từ:

- Đỉnh (S): Là một điểm duy nhất không thuộc mặt phẳng đáy, nơi tất cả các cạnh bên cùng gặp nhau. Đây chính là điểm hội tụ quyền lực, tạo nên hình dáng cao vút đặc trưng.
- Chiều cao (h): Là khoảng cách từ đỉnh S xuống mặt phẳng chứa đáy. Đây là yếu tố cốt lõi trong mọi công thức hình chóp liên quan đến thể tích.
- Mặt đáy: Là một đa giác bất kỳ (tam giác, tứ giác, ngũ giác…). Hình dáng của mặt đáy sẽ quyết định “tên gọi” của hình chóp (hình chóp tam giác, hình chóp tứ giác…).
- Các mặt bên: Luôn là những hình tam giác có chung đỉnh S. Những mặt bên này nghiêng đều, cùng hướng về đỉnh, tạo nên sự vững chắc cho toàn bộ cấu trúc.
Hiểu rõ những thành phần này chính là bước đầu tiên. Để việc học và áp dụng các công thức hình chóp trở nên trực quan và dễ dàng hơn rất nhiều.
Phân loại hình chóp từ đơn giản đến phức tạp
Thế giới của hình chóp rất đa dạng. Tuy nhiên, chúng ta thường gặp nhất là “hình chóp đều”.
- Hình chóp đều: Là hình chóp có đáy là một đa giác đều (tam giác đều, hình vuông…) và chân đường cao trùng với tâm của đa giác đáy. Đặc điểm này mang lại sự cân đối hoàn hảo, và việc áp dụng công thức hình chóp cho loại này cũng có phần ưu ái hơn.
- Hình chóp thường: Là các trường hợp còn lại, đáy có thể là một đa giác bất kỳ và chân đường cao không nhất thiết phải là tâm của đáy.
Việc phân loại này quan trọng vì nó ảnh hưởng đến cách chúng ta tính toán diện tích đáy. Đôi khi là cách xác định các yếu tố khác trong công thức hình chóp.
Bộ công thức hình chóp kinh điển
Bây giờ, chúng ta đã sẵn sàng bước vào phần cốt lõi, nơi những con số bắt đầu lên tiếng. Đây là những công cụ quyền năng giúp bạn đo lường, tính toán và thực sự làm chủ khối hình học này.
Công thức thể tích hình chóp (v) đo lường
Đây có lẽ là công thức hình chóp nổi tiếng và được ứng dụng nhiều nhất. Nó cho chúng ta biết “sức chứa” của hình chóp, tức toàn bộ không gian bên trong nó. Công thức như sau: V = ⅓ B . h
Giải thích chi tiết:
- V: Là thể tích của hình chóp.
- B: Là diện tích mặt đáy (Base Area). Tùy vào đáy là hình gì (tam giác, vuông, chữ nhật…) mà ta sẽ áp dụng công thức tính diện tích tương ứng.
- h: Là chiều cao của hình chóp (khoảng cách từ đỉnh xuống mặt phẳng đáy).
Yếu tố “1/3” trong công thức hình chóp này là một hằng số toán học kỳ diệu. Nó cho thấy rằng, với cùng một diện tích đáy và cùng một chiều cao, thể tích của một hình chóp luôn luôn chỉ bằng một phần ba thể tích của một hình lăng trụ tương ứng. Đây là một phát hiện vĩ đại của các nhà toán học cổ đại. Để vận dụng đúng công thức này, việc xác định chính xác diện tích đáy và chiều cao là hai nhiệm vụ tiên quyết.
Công thức diện tích xung quanh và toàn phần
Nếu công thức thể tích giúp ta nhìn vào “bên trong”, thì bộ đôi công thức hình chóp về diện tích lại giúp ta đo lường “bên ngoài” – bề mặt của khối chóp.
Về diện tích xung quanh (Sxq): Diện tích xung quanh được tính như thế nào vẫn đang nhận được nhiều sự quan tâm. Đây là tổng diện tích của tất cả các mặt bên (các mặt tam giác).
- Với hình chóp thường: Sxq= Tổng diện tích mặt các bên. Bạn phải tính từng mặt tam giác rồi sau đó cộng lại.
- Với hình chóp đều (công thức đặc biệt): Sxq=p⋅d

Giải thích chi tiết: p: Là nửa chu vi đáy. d: Là trung đoạn (Slant Height) – tức chiều cao của một mặt bên, kẻ từ đỉnh S. Lưu ý cực kỳ quan trọng là không được nhầm lẫn trung đoạn (d) với chiều cao của hình chóp (h). Đây là lỗi sai phổ biến nhất khi áp dụng công thức hình chóp này.
Diện tích toàn phần (Stp): Đây là công thức đơn giản nhất về mặt logic: diện tích toàn phần chính là tổng của diện tích xung quanh và diện tích đáy.
Stp=Sxq+B
Việc nắm vững bộ đôi công thức hình chóp này cực kỳ hữu ích khi bạn cần tính toán lượng vật liệu cần thiết để che phủ hoặc sơn phết bề mặt của một vật thể có hình chóp.
Xem thêm: Tính Thể Tích Hình Cầu – Từ Lý Thuyết Đến Bài Toán Thực Tế
Ứng dụng kỳ diệu khi công thức hình chóp bước ra đời thực
Toán học sẽ trở nên vô nghĩa nếu chỉ nằm trên giấy. Sức mạnh thực sự của chúng nằm ở khả năng ứng dụng vô tận của nó trong thế giới thực. Từ những công trình vĩ đại đến những vật dụng nhỏ bé.
Kiến trúc xây dựng những biểu tượng
Đây là lĩnh vực mà công thức hình chóp thể hiện quyền năng của nó một cách rõ ràng nhất. Chúng ta có thể thấy ứng dụng của nó ở khắp mọi nơi từ cổ đại đến hiện đại.
- Kim Tự Tháp Ai Cập: Các kỹ sư cổ đại, dù chưa viết ra công thức tường minh như chúng ta ngày nay, nhưng chắc chắn đã nắm được tỷ lệ vàng giữa các yếu tố. Việc tính toán thể tích đá cần thiết để xây dựng một kim tự tháp khổng lồ chính là một bài toán áp dụng công thức ở quy mô lớn nhất.
- Kiến trúc hiện đại: Mái của nhiều nhà thờ, tháp chuông, hay các tòa nhà chọc trời có phần đỉnh hình chóp đều cần đến các tính toán chính xác. Các kiến trúc sư sử dụng công thức hình chóp về diện tích để tính lượng kính, ngói, hay tấm lợp kim loại cần dùng. Một giải thích chi tiết hơn là họ còn dùng nó để tính toán tải trọng gió và áp lực lên bề mặt mái.
Thiết kế bao bì và công nghiệp
Bạn có để ý những hộp sôcôla, những lọ nước hoa hay thậm chí một số loại lều cắm trại có hình chóp không? Các nhà thiết kế sản phẩm sử dụng công thức hình chóp để:
- Tối ưu hóa vật liệu: Tính toán chính xác diện tích bìa carton hay nhựa cần dùng để sản xuất một chiếc hộp, tránh lãng phí.
- Xác định dung tích: Dùng công thức thể tích để đảm bảo lọ nước hoa chứa đúng 50ml hay hộp sữa chứa đúng 1 lít.
Mỗi một sản phẩm đẹp mắt và vừa vặn trên kệ hàng đều có thể là kết quả của việc áp dụng chính xác một công thức hình chóp.
Công thức hình chóp ở khoa học tự nhiên & địa chất
Ngay cả trong tự nhiên, hình chóp cũng xuất hiện. Các nhà địa chất có thể ước tính thể tích của một ngọn núi lửa hình nón (một dạng hình chóp với đáy tròn) bằng cách sử dụng một biến thể của công thức cơ bản. Điều này giúp họ nghiên cứu về trữ lượng khoáng sản hoặc dự báo các hoạt động địa chất.
Lời kết
Công thức hình chóp không chỉ là những ký tự và con số khô khan. Nó là cây cầu nối liền giữa ý tưởng và hiện thực, giữa lý thuyết hình học và những ứng dụng thực tiễn đầy cảm hứng. Theo kpophoto thấy khi nắm vững nó trong tay cũng đồng nghĩa với việc bạn đang nắm giữ một trong những công cụ mạnh mẽ nhất. Để hiểu và kiến tạo nên thế giới ba chiều xung quanh mình.