Công thức logarit là nền tảng quan trọng trong chương trình Đại số & Giải tích lớp 12. Việc ghi nhớ công thức thôi chưa đủ; học sinh cần hiểu rõ cách áp dụng, kết hợp với tư duy giải nhanh để xử lý bài toán một cách logic, hiệu quả. Bài viết này kpophoto trình bày đầy đủ hệ thống công thức kèm phân tích chuyên sâu.
Hệ thống công thức logarit cơ bản, mở rộng
Logarit không chỉ là công cụ tính toán mà còn là chìa khóa giải quyết nhiều bài toán phức tạp trong đại số, giải tích. Hiểu rõ bản chất từng công thức giúp vận dụng linh hoạt, tiết kiệm thời gian khi làm bài.
Công thức logarit cơ bản tích, thương, lũy thừa
Ba công thức logarit nền tảng gồm: logarit của tích số, thương số, lũy thừa là nền móng để biến đổi biểu thức. Cụ thể:
- loga(x.y)=logax+logay
- loga(x/y)=logax−logay
- loga(x^n)=n.logax
Các công thức logarit này không chỉ là quy tắc thao tác máy móc mà còn phản ánh tính chất hàm số logarit. Sự tương đồng giữa logarit, các phép toán đại số giúp tạo cầu nối giữa suy luận hình thức, bản chất toán học.
Một trong những ưu điểm lớn của các công thức cơ bản là khả năng kết hợp linh hoạt. Ta có thể đồng thời dùng cả ba trong một biểu thức để đạt tới mục tiêu rút gọn tối ưu.
Việc sử dụng đúng ngữ cảnh của từng công thức đòi hỏi người học phải quan sát biểu thức cẩn thận. Nếu lẫn lộn giữa logarit tích, lũy thừa, rất dễ dẫn đến sai số ngay từ bước đầu tiên.

Trong các đề thi chuẩn hóa hoặc kiểm tra học kỳ, nhóm công thức này luôn chiếm một tỷ trọng đáng kể. Thành thạo cách áp dụng chúng sẽ giúp tiết kiệm đáng kể thời gian xử lý bài toán.
Một lỗi phổ biến là quên đặt điều kiện xác định trước khi biến đổi, khiến kết quả sai lệch hoặc vô nghĩa. Khi thành thạo, người học có thể chuyển đổi linh hoạt giữa các dạng biểu thức để phù hợp yêu cầu đề bài.
Biến đổi logarit về cùng cơ số
Đổi cơ số là kỹ thuật quan trọng để đưa các biểu thức về dạng có thể cộng, trừ hoặc so sánh. Công thức phổ biến: logbx=logax/logab. Cách làm này giúp đồng nhất biểu thức, đặc biệt trong những bài cần xét dấu hoặc bất phương trình logarit.
Khi cơ số đồng nhất, các bước tiếp theo sẽ dễ phân tích, áp dụng công thức. Học sinh thường nhầm thứ tự của tử, mẫu trong công thức đổi cơ số. Chỉ một sai sót nhỏ có thể kéo theo loạt phép biến đổi sai lầm về sau.
Công thức logarit nâng cao, dạng tổng quát
Một số bài toán yêu cầu sử dụng tổ hợp công thức hoặc vận dụng logarit nhiều tầng. Ví dụ: biểu thức dạng loga(logbx) đòi hỏi biến đổi từng lớp theo quy tắc cơ bản.
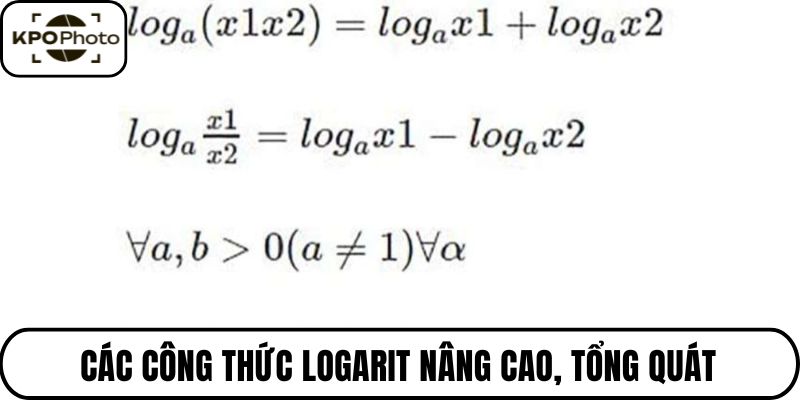
Đối với dạng công thức logarit tổng quát như logf(x)(g(x)), việc xét điều kiện xác định, đạo hàm hàm hợp cũng cần được cân nhắc. Những công thức này thường xuất hiện trong đề thi có mức độ phân loại cao.
Một hướng khai thác nâng cao là liên kết logarit với các giới hạn hoặc tích phân khi giải quyết bài toán hàm số. Đó cũng là tiền đề khi bước sang giải tích hiện đại hơn.
Xem thêm: Hàm Số Bậc Nhất – Ứng Dụng Và Bản Chất Trong Thực Tế
Tư duy giải nhanh qua các dạng bài logarit
Tư duy giải nhanh trong logarit không đơn thuần chỉ là ghi nhớ công thức, mà còn phụ thuộc vào khả năng nhận diện cấu trúc bài toán, lựa chọn phương pháp tiếp cận phù hợp. Mỗi dạng bài sẽ có hướng xử lý riêng, đòi hỏi người học phải linh hoạt, có nền tảng suy luận vững chắc.
Cách nhìn bài để chọn phương pháp rút gọn hiệu quả
Khi gặp công thức logarit, điều đầu tiên cần làm là quan sát tổng thể để phát hiện điểm chung về cơ số, biến số hay dạng đối xứng. Những yếu tố này sẽ gợi ý cách rút gọn hoặc nhóm lại để áp dụng công thức kinh điển.
Chẳng hạn, nếu các logarit trong biểu thức có cùng cơ số, biến dạng tích, ta nên dùng công thức cộng logarit để gom lại. Trong trường hợp các hạng tử có dấu trừ, phép chia thường là bản chất ẩn đằng sau cần được khai thác.
Đôi khi biểu thức được trình bày dài dòng nhằm mục đích đánh lạc hướng, trong khi bản chất có thể đơn giản hóa chỉ qua một bước rút gọn. Điều này xảy ra khá phổ biến trong các đề thi trắc nghiệm phân loại cao.
Một mẹo nhỏ giúp xử lý nhanh là thử khai triển từng logarit theo hướng ngược lại: từ logarit tổng hợp về logarit thành phần. Cách làm này không cần suy luận quá phức tạp, chỉ yêu cầu thành thạo công thức cơ bản.

Bài toán chứa các hằng số quen thuộc như log₂8, log₃27 thường ẩn giấu khả năng rút gọn về số nguyên. Khi nhận ra điều này, học sinh có thể tránh được việc sa lầy vào các phép tính không cần thiết.
Đối với biểu thức chứa căn thức hoặc số mũ, ưu tiên biến đổi về dạng bình thường rồi mới xét logarit. Điều này giúp tránh sai sót khi áp dụng công thức logarit cho biểu thức phức tạp.
Tư duy ngược từ đáp án suy ra điều kiện
Trong bài trắc nghiệm, đáp án là công cụ quan trọng để rút ngắn thời gian làm bài nếu biết cách khai thác. Thay vì giải từ đầu, ta có thể thử thế từng phương án vào biểu thức gốc để kiểm tra tính đúng đắn.
Phương pháp này đặc biệt hiệu quả khi đề bài không yêu cầu giải toàn bộ, mà chỉ cần xác định đáp án đúng. Những biểu thức phức tạp, dài dòng có thể xử lý gọn hơn rất nhiều nếu đi từ đích đến nguồn.
Một kỹ thuật khác là dùng điều kiện xác định để loại nhanh đáp án không hợp lệ. Logarit không xác định với số âm hoặc số không, nên chỉ cần kiểm tra điều kiện xác định là có thể loại một phần phương án.
Có những trường hợp, chỉ cần xét dấu của mẫu số hoặc giá trị của cơ số cũng đủ để kết luận đáp án nào bị loại bỏ. Việc này không những tiết kiệm thời gian mà còn giảm thiểu sai sót do thao tác tính toán.

Phân tích điểm mấu chốt trong công thức logarit – như cơ số hoặc phần tử trong ngoặc log – thường giúp dự đoán nhanh kết quả gần đúng. Tư duy kiểu này cần luyện tập nhiều để trở thành phản xạ.
Cũng cần lưu ý rằng không phải bài nào cũng áp dụng được phương pháp thế ngược, nhất là khi có quá nhiều biến hoặc dạng ẩn. Khi đó, người học phải kết hợp song song cả tư duy tiến, lùi để tìm ra hướng giải phù hợp.
Ưu tiên đổi cơ số hay biến đổi công thức logarit?
Việc lựa chọn đổi cơ số hay biến đổi biểu thức phụ thuộc nhiều vào dạng bài, mức độ đồng nhất trong biểu thức. Nếu cơ số đồng nhất, việc rút gọn sẽ trở nên dễ dàng hơn rất nhiều khi áp dụng các công thức cộng trừ logarit.
Trong trường hợp biểu thức chứa nhiều logarit với cơ số khác nhau, đổi toàn bộ về cùng một cơ số là chiến lược thường được ưu tiên. Cơ số 10 hoặc cơ số e thường được chọn do quen thuộc, dễ xử lý bằng máy tính.
Tuy nhiên, nếu sau khi đổi cơ số công thức logarit trở nên phức tạp hơn, cần cân nhắc quay lại hướng rút gọn trực tiếp. Nhiều bài toán có thể khai thác ngay từ các mẫu quen thuộc như log₄(2), log₈(16) mà không cần đổi.
Trong bài toán phương trình, đổi cơ số giúp đưa biểu thức về dạng đại số dễ giải, ví dụ biến phương trình logarit thành phương trình bậc hai. Đây là điểm mấu chốt để giải bài chính xác mà không cần lập hệ.
Một sai lầm phổ biến là đổi cơ số một cách máy móc mà không phân tích xem đổi xong có lợi hay không. Việc này khiến công thức logarit rối rắm hơn, dẫn đến mất phương hướng khi tiếp tục giải.
Trong mọi trường hợp, nên quan sát biểu thức một lượt để xác định đâu là bước đi ngắn nhất. Đôi khi chỉ một thay đổi nhỏ cũng giúp rút ngắn quá trình biến đổi từ ba bước xuống còn một.
Kết luận
Công thức logarit không chỉ là kiến thức trọng tâm của chương trình Đại số & Giải tích mà còn là công cụ giải quyết nhiều bài toán phức tạp. Việc hiểu rõ cấu trúc công thức, tránh sai lầm thường gặp, rèn luyện tư duy giải nhanh sẽ giúp học sinh xử lý các dạng bài toán một cách hiệu quả, chính xác, tiết kiệm thời gian.

