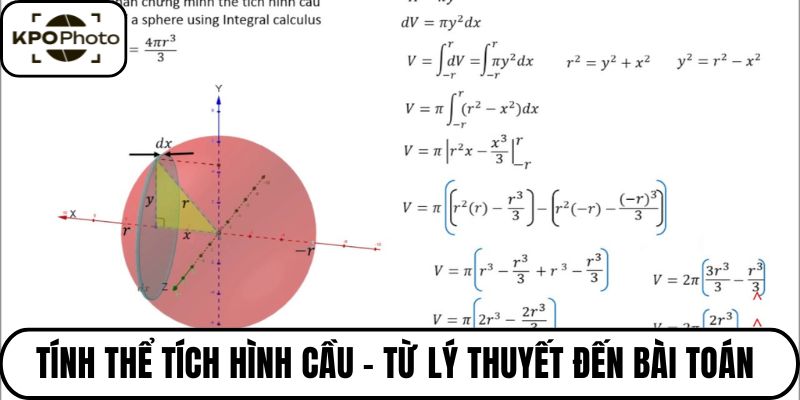
Tính thể tích hình cầu không chỉ là một bài toán trong sách giáo khoa. Mà kpophoto thấy nó là cánh cổng dẫn chúng ta đến việc đo lường một trong những hình khối đẹp và phổ biến nhất trong vũ trụ. Từ giọt sương long lanh trên chiếc lá, bong bóng xà phòng mỏng manh bay trong gió. Cho đến những hành tinh khổng lồ trong dải ngân hà, hình cầu hiện diện như một biểu tượng của sự cân đối và toàn vẹn tuyệt đối.
Vài nét giới thiệu về hình cầu
Trước khi chúng ta đi sâu vào những con số và công thức, hãy dành một khoảnh khắc để cảm nhận vẻ đẹp của hình cầu. Nó là một khối hình học đặc biệt không có góc cạnh, không có đỉnh, chỉ có một bề mặt cong hoàn hảo và duy nhất.
Mọi điểm trên bề mặt của nó đều cách đều một điểm cố định duy nhất gọi là tâm. Chính sự đơn giản mà hoàn mỹ này khiến cho việc tính thể tích hình cầu trở thành một bài toán vừa thanh lịch vừa quan trọng.
Tìm hiểu yếu tố tâm và bán kính ở hình cầu
Để chinh phục được bài toán tính thể tích hình cầu bạn chỉ cần nắm vững một vài yếu tố nền tảng, trong đó quan trọng nhất chính là “bán kính”. Việc xác định chính xác thông số này là bước đầu tiên và then chốt trong mọi quy trình tính toán. Các thành phần đó bao gồm:

- Tâm (O): Là điểm gốc, trái tim của hình cầu. Mọi thứ đều xoay quanh nó.
- Bán kính (r): Là khoảng cách từ tâm đến bất kỳ điểm nào trên bề mặt hình cầu. Đây là thông số vàng, là chìa khóa duy nhất bạn cần để mở ra cánh cửa của công thức tính thể tích hình cầu.
- Đường kính (d): Là khoảng cách lớn nhất giữa hai điểm trên bề mặt hình cầu, nó luôn đi qua tâm và có độ dài bằng hai lần bán kính (d = 2r).
Công thức vàng hé lộ bí mật thể tích
Giờ là lúc chúng ta đi vào trọng tâm của vấn đề. Có một công thức toán học duy nhất, vô cùng mạnh mẽ và thanh lịch, được sinh ra để giải quyết bài toán tính thể tích.
Công thức tính thể tích hình cầu (V)
Công thức này được các nhà toán học vĩ đại như Archimedes tìm ra và chứng minh, và nó vẫn còn nguyên giá trị cho đến ngày nay. Hãy cùng phân tích chi tiết công thức kỳ diệu này:
V = 4/3πr3
Trong đó:
- V: Ký hiệu cho thể tích, là lượng không gian mà hình cầu chiếm giữ.
- 4/3: Một hằng số toán học đặc biệt. Sự xuất hiện của nó là kết quả của các phép tính tích phân cao cấp để tìm ra công thức này, cho thấy mối liên hệ sâu sắc giữa hình cầu và các hình khối khác.
- π (Pi): Hằng số Pi (xấp xỉ 3.14159…) là “linh hồn” của các hình khối tròn. Nó biểu thị tỷ lệ giữa chu vi và đường kính của một đường tròn. Sự có mặt của Pi trong công thức tính thể tích hình cầu là điều tất yếu.
- r³ (bán kính lập phương): Đây là trái tim của công thức. Thể tích là một đại lượng không gian 3 chiều, vì vậy bán kính (đại lượng 1 chiều) phải được lũy thừa 3. Điều này hoàn toàn logic! Sức mạnh của công thức nằm ở sự đơn giản đến kinh ngạc: chỉ cần biết bán kính, bạn có thể biết mọi thứ.
Hướng dẫn từng bước để tính thể tích hình cầu
Để biến công thức từ lý thuyết thành thực hành, bạn chỉ cần làm theo 3 bước đơn giản sau đây. Đây là quy trình chuẩn, giúp bạn giải quyết mọi bài toán tính thể tích hình cầu một cách dễ dàng.
- Xác định bán kính (r): Tìm giá trị bán kính của hình cầu. Nếu đề bài cho đường kính (d), hãy nhớ chia đôi để tìm bán kính (r = d/2).
- Lập phương bán kính: Tính giá trị của r³. Tức là lấy r nhân với chính nó 3 lần (r × r × r).
- Nhân với các hằng số: Lấy kết quả vừa tính được nhân với π và nhân tiếp với 4/3 để ra kết quả cuối cùng.
Xem thêm: Tính Thể Tích Hình Cầu Chính Xác, Cách Ghi Nhớ Công Thức
Minh họa thực tế trong cuộc sống
Nếu bạn nghĩ rằng công thức này chỉ tồn tại trong các kỳ thi, bạn sẽ phải ngạc nhiên về mức độ phổ biến và tầm quan trọng của nó. Việc tính thể tích hình cầu là một kỹ năng được ứng dụng trong vô số lĩnh vực.
Thiên văn học – Đo lường cả vũ trụ
Đây là minh họa thực tế hùng vĩ nhất. Các nhà thiên văn học không thể dùng thước để đo các hành tinh, nhưng họ có thể quan sát và ước tính bán kính của chúng. Từ đó:
- Họ áp dụng công thức để tìm ra thể tích của Trái Đất, Sao Hỏa hay Sao Mộc.
- Kết hợp với khối lượng, việc tính thể tích hình cầu cho phép họ suy ra mật độ của một hành tinh, từ đó phỏng đoán về cấu tạo lõi của nó (đá, khí, hay kim loại).
- Công việc này là nền tảng để hiểu về sự hình thành và phát triển của các hệ sao.
Từ những chi tiết nhỏ nhất của kỹ thuật và sản xuất
Trong ngành kỹ thuật, độ chính xác là tất cả. Các ứng dụng của việc tính thể tích là vô cùng đa dạng và quan trọng.

- Vòng bi (Ball Bearings): Hàng triệu viên bi thép nhỏ hình cầu hoàn hảo là bộ phận không thể thiếu trong hầu hết các máy móc, từ xe đạp đến động cơ máy bay. Các kỹ sư phải tính thể tích hình cầu của chúng để tính toán khối lượng, vật liệu cần dùng và khả năng chịu tải.
- Bồn chứa hình cầu: Các bồn chứa khí hóa lỏng (LNG) hay khí gas (LPG) thường có dạng hình cầu. Đây là minh họa thực tế cho thấy hình cầu là hình dạng tối ưu nhất để chứa một thể tích lớn nhất với diện tích bề mặt nhỏ nhất, giúp tiết kiệm vật liệu và chịu được áp suất cao. Việc tính thể tích hình cầu chính xác là tối quan trọng để đảm bảo an toàn và hiệu quả.
Y học – Nhìn thấu bên trong cơ thể
Trong y học, khả năng tính đôi khi mang ý nghĩa sống còn. Khi phân tích hình ảnh từ máy chụp CT hoặc MRI, các bác sĩ có thể xác định một khối u gần có dạng hình cầu.
Bằng cách đo bán kính của nó, họ có thể tính thể tích hình cầu để ước tính kích thước khối u. Sau đó theo dõi sự phát triển của nó qua thời gian và quyết định phương pháp điều trị phù hợp. Đây là một minh họa cho thấy toán học đang phục vụ trực tiếp cho sức khỏe con người.
Ẩm thực và đời sống hàng ngày thú vị
Bạn có nghĩ trong ngăn bếp quen thuộc của bạn vẫn hiện hữu các công thức thú vị chưa?Câu trả lời là có, công thức này luôn hiện diện một cách đầy ngạc nhiên!
- Khi bạn dùng muỗng múc một viên kem tròn xoe, bạn đang tạo ra một hình cầu. Việc tính thể tích hình cầu có thể giúp các nhà sản xuất kem xác định chính xác lượng calo trong mỗi muỗng kem.
- Một viên kẹo sô-cô-la truffle, một viên thịt viên, hay một quả cam… tất cả đều có thể được ước tính thể tích bằng công thức này. Đây là những ví dụ gần gũi cho thấy toán học không hề xa vời.
Lời kết
Tính thể tích hình cầu là một cây cầu diệu kỳ nối liền thế giới toán học trừu tượng với vô vàn ứng dụng thực tiễn. Từ việc khám phá những bí mật của vũ trụ bao la cho đến việc đảm bảo an toàn cho một cỗ máy hay thậm chí là tính toán khẩu phần ăn. Kpophoto thấy việc nắm vững nó chính là bạn đang sở hữu một công cụ mạnh mẽ.