Tính thể tích hình cầu là một kiến thức quan trọng trong chương trình hình học không gian. Nắm rõ công thức này không chỉ giúp giải nhanh bài tập mà còn hỗ trợ tư duy về khối tròn xoay trong thực tế. Bài viết dưới đây, kpophoto sẽ hướng dẫn bạn cách áp dụng công thức chính xác, chia sẻ mẹo ghi nhớ cực kỳ dễ nhớ, dễ áp dụng.
Tính thể tích hình cầu – Công thức đầy đủ, chuẩn xác
Để làm chủ kiến thức về thể tích hình cầu, trước tiên bạn cần nắm vững công thức tính một cách chắc chắn, chính xác.
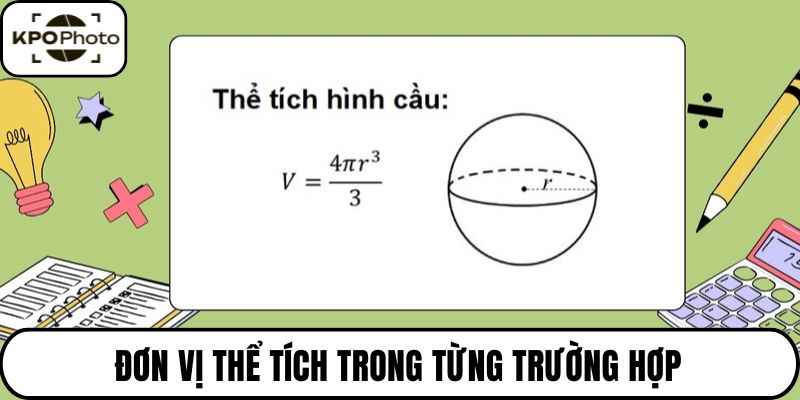
Biểu thức tính thể tích hình cầu V = 4/3 π r³
Công thức chuẩn để tính thể tích hình cầu được biểu diễn là: V = 4/3 × π × r³. Trong đó,ký tự π là được gọi là hằng số pi (xấp xỉ 3.14), còn r là bán kính của hình cầu.

Đây là một biểu thức quan trọng giúp bạn xác định lượng không gian mà một khối cầu chiếm trong không gian ba chiều. Dù đơn giản nhưng công thức này lại ứng dụng rộng rãi trong nhiều lĩnh vực, từ toán học thuần túy đến vật lý hay kỹ thuật.
Giải thích ý nghĩa từng thành phần trong công thức
Trong công thức tính thể tích hình cầu, hằng số 4/3 phản ánh mối quan hệ đặc trưng giữa hình cầu, hình lập phương chứa nó. Đây không phải là con số ngẫu nhiên mà được suy ra từ quá trình tích phân trong giải tích không gian.
Phần r³ cho biết thể tích tỉ lệ với lập phương của bán kính — nghĩa là khi bán kính tăng gấp đôi, thể tích sẽ tăng gấp tám lần. Điều này cho thấy sự nhạy cảm của thể tích với kích thước của hình cầu.
Đơn vị thể tích phù hợp trong từng trường hợp
Nếu bán kính được tính bằng cm, thể tích sẽ mang đơn vị là cm³; tương tự, bán kính tính bằng mét thì thể tích sẽ là m³. Việc thống nhất đơn vị giúp tránh sai sót trong các phép tính liên quan đến thể tích.
Trong các bài toán thực tế như tính thể tích trái bóng hay khối cầu trong kỹ thuật, việc lựa chọn đúng đơn vị còn giúp đảm bảo độ chính xác của kết quả cuối cùng.
Hướng dẫn cách ghi nhớ công thức đơn giản mà hiệu quả
Để ghi nhớ công thức tính thể tích hình cầu một cách hiệu quả, bạn nên áp dụng các phương pháp gắn kết với trí tưởng tượng, liên hệ kiến thức có sẵn, khai thác kỹ thuật ghi nhớ khoa học. Các mẹo sau đây kpophoto sẽ giúp bạn nhớ công thức một cách tự nhiên, dễ dàng, lâu dài.
Sử dụng quy tắc tính thể tích hình cầu hình ảnh, câu chuyện
Trí nhớ của con người thường phản ứng tốt với hình ảnh sinh động hơn là con số khô khan, vì vậy việc chuyển công thức thành hình ảnh trực quan là một mẹo rất hữu ích. Hãy tưởng tượng một quả bóng khổng lồ được “nén lại” bởi ba lực từ bên ngoài, chia thành bốn phần bằng nhau — bạn sẽ liên tưởng được đến tỷ lệ 4/3 trong công thức.
Ngoài ra, hãy thử tạo một câu chuyện ngắn để mã hóa công thức: “Một ngày nọ, R – cậu bé robot có bán kính siêu năng – quyết định quay ba vòng quanh chiếc bánh pizza khổng lồ của π, rồi chia nó thành bốn phần để chia cho nhóm bạn không gian.” Dù ngớ ngẩn, chính yếu tố hài hước, hình tượng đó sẽ giúp bạn không thể quên được biểu thức V = 4/3 π r³.
Bạn cũng có thể vẽ biểu đồ thể hiện thể tích các khối tròn xoay (nón, trụ, cầu) để thấy được mối quan hệ thị giác giữa chúng. Việc sử dụng hình ảnh màu sắc kết hợp công thức sẽ làm tăng hiệu quả ghi nhớ qua não phải – trung tâm xử lý trực quan của con người.
Không chỉ học để nhớ, việc “kể lại” công thức qua hình ảnh hoặc câu chuyện còn giúp bạn dễ truyền đạt kiến thức cho người khác. Khi đã có khả năng diễn giải, bạn đã thực sự ghi nhớ sâu sắc, hiểu bản chất vấn đề.
Mẹo học thuộc bằng phương pháp lặp lại ngắt quãng
Đây là một kỹ thuật học tập dựa trên nguyên lý ghi nhớ lâu dài nhờ vào việc ôn lại kiến thức theo chu kỳ thời gian được giãn dần. Thay vì học đi học lại liên tục trong một buổi, hãy học công thức một lần, sau đó ôn lại vào ngày hôm sau, rồi tiếp tục sau 3 ngày, 1 tuần,… điều này giúp chuyển thông tin vào trí nhớ dài hạn.
Ví dụ, bạn có thể học công thức vào sáng thứ Hai, nhắc lại vào tối thứ Ba, kiểm tra lại sáng thứ Sáu, ôn lại vào thứ Hai tuần sau. Sau mỗi lần ôn, bạn cố gắng viết lại công thức mà không nhìn tài liệu, so sánh để điều chỉnh nếu sai.
Một mẹo hay là viết công thức ra giấy nhớ, dán ở những nơi bạn thường xuyên nhìn thấy như bàn học, cửa tủ, hoặc màn hình máy tính. Sự lặp lại trong môi trường sẽ khiến bộ não tiếp nhận thông tin một cách tự nhiên mà không cần phải cố nhớ.
Bạn cũng có thể kết hợp lặp lại ngắt quãng với hình ảnh, câu chuyện đã tạo trước đó để làm quá trình ghi nhớ trở nên nhẹ nhàng hơn. Cứ mỗi lần lặp lại, bạn không chỉ nhớ công thức mà còn hình dung ra cả bối cảnh, câu chuyện gắn liền với nó.
Liên kết công thức tính thể tích hình cầu với các hình học khác
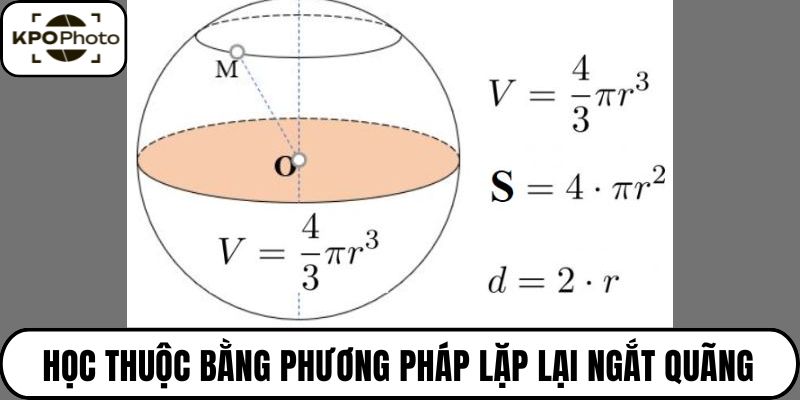
Một trong những cách học thông minh là đặt công thức trong hệ thống kiến thức, thay vì xem nó như một mảnh rời rạc. Hãy nhìn lại công thức thể tích hình nón (V = 1/3 π r² h) hay hình trụ (V = π r² h), bạn sẽ thấy rõ rằng những công thức này cùng chung yếu tố π, r, chỉ khác nhau ở yếu tố tỷ lệ, chiều cao.
Việc này giúp bạn hiểu công thức V = 4/3 π r³ không đơn thuần là một biểu thức riêng biệt, mà là sự phát triển tự nhiên của các công thức thể tích khối tròn xoay khi chuyển từ khối có chiều cao xác định (trụ, nón) sang khối có kích thước đồng nhất mọi chiều (cầu).
Khi bạn nhận thấy rằng hình cầu là “biến thể tròn trịa” nhất của các hình xoay quanh trục, bạn sẽ dễ ghi nhớ sự khác biệt của nó — thay vì có chiều cao, nó “gói gọn” toàn bộ thể tích vào bán kính. Nhờ đó, bạn không cần học thuộc máy móc, mà chỉ cần hiểu cách khối cầu được xây dựng từ logic hình học.

Ngoài ra, khi làm các bài tập liên quan đến nhiều hình khối kết hợp, việc nhớ đúng công thức, mối liên hệ giữa chúng sẽ giúp bạn giải bài nhanh chóng. Đây là lợi thế lớn trong các kỳ thi yêu cầu tư duy phân tích hình học không gian.
Xem thêm: Công Thức Hình Chóp, Mẹo Tư Duy Giải Nhanh Hiệu Quả
Những lỗi thường gặp, mẹo xử lý khi tính thể tích hình cầu
Trong quá trình tính thể tích hình cầu, học sinh dễ mắc phải một số sai sót cơ bản làm ảnh hưởng đến kết quả cuối cùng. Nhận diện đúng lỗi, áp dụng mẹo xử lý phù hợp sẽ giúp bạn tránh mất điểm đáng tiếc.
- Một trong những lỗi phổ biến nhất là nhầm lẫn giữa bán kính, đường kính. Khi đề bài cho đường kính nhưng người học lại thay trực tiếp vào công thức mà không chia đôi sẽ khiến kết quả sai lệch hoàn toàn.
- Ngoài ra, việc quên nhân với hằng số π cũng là lỗi thường gặp, đặc biệt trong quá trình nhập máy tính. Để khắc phục, hãy luôn viết lại công thức đầy đủ trước khi thay số, điều này giúp bạn kiểm tra nhanh, hạn chế bỏ sót yếu tố quan trọng.
- Một lỗi khác là sử dụng sai đơn vị đo, dẫn đến kết quả không phù hợp với yêu cầu đề bài. Khi gặp bài toán có đơn vị khác nhau như cm, dm hoặc m, hãy đổi về cùng một đơn vị trước khi tính để đảm bảo độ chính xác.
- Nhiều học sinh cũng thường quên viết đơn vị cho kết quả cuối cùng, nhất là trong các bài kiểm tra trắc nghiệm. Mẹo ở đây là luôn ghi nhớ: thể tích phải kèm đơn vị lập phương như cm³ hoặc m³ để thể hiện sự hiểu biết đầy đủ.
Kết luận
Tính thể tích hình cầu không còn là thử thách nếu bạn hiểu rõ công thức, nắm được cách ghi nhớ phù hợp. Hy vọng với các mẹo ghi nhớ, cách tránh lỗi phổ biến được kpophoto chia sẻ, bạn sẽ tự tin hơn khi làm việc với các bài toán hình học không gian.

