Hàm số bậc nhất là một trong những kiến thức nền tảng của Đại số trung học phổ thông. Đây là loại hàm có dạng tổng quát đơn giản nhưng mang lại nhiều ý nghĩa trong học tập, đời sống. Bài viết này kpophoto phân tích từ lý thuyết đến minh họa thực tế nhằm hỗ trợ học sinh tiếp cận bài bản và chắc chắn hơn.
Hàm số bậc nhất – Khái niệm với dạng tổng quát
Hàm số bậc nhất được định nghĩa là hàm có dạng y=ax+b, trong đó a, b là các hằng số, a≠0. Biến số x nằm trong tập hợp số thực, là yếu tố thay đổi duy nhất ảnh hưởng đến giá trị của hàm.
Thành phần aaa được gọi là hệ số góc, quyết định độ nghiêng của đồ thị trên mặt phẳng tọa độ. Trong khi đó, bbb đóng vai trò là hệ số tự do, biểu thị điểm cắt trục tung của đồ thị hàm.
Không giống hàm hằng hay hàm bậc hai, hàm số bậc nhất cho đồ thị là một đường thẳng đơn. Sự đơn giản trong cấu trúc lại tạo điều kiện thuận lợi cho việc áp dụng vào các tình huống tính toán thực tế.

Đây là loại hàm đầu tiên học sinh được tiếp cận khi bắt đầu chương trình đại số mang tính hình học. Vì vậy, việc nắm chắc bản chất của nó không chỉ giúp giải bài tập mà còn là nền tảng cho các kiến thức phức tạp hơn sau này.
Tính chất của hàm số bậc nhất
Để hiểu sâu hàm số bậc nhất, cần xét các đặc điểm hình học, đại số tiêu biểu của nó. Trong phần này, kpophoto sẽ lần lượt trình bày các khía cạnh quan trọng qua từng tính chất cụ thể.
Tính đồng biến và nghịch biến
Một trong những biểu hiện đặc trưng của hàm bậc nhất là sự thay đổi đều đặn của giá trị hàm theo chiều của biến số. Dựa vào dấu của hệ số a trong công thức y=ax+b, ta dễ dàng nhận biết tính đồng biến hoặc nghịch biến.
Cụ thể, nếu a>0, hàm số sẽ đồng biến trên toàn bộ tập xác định, tức là giá trị hàm tăng khi biến số tăng. Trường hợp a<0 thì hàm lại nghịch biến, nghĩa là giá trị hàm giảm khi biến tăng.
Tính chất này được thể hiện rõ rệt qua đồ thị: đường thẳng đi lên khi hệ số dương, đi xuống nếu hệ số âm. Không có ngoại lệ hoặc điểm đặc biệt nào khiến tính chất bị gián đoạn trong quá trình biến thiên.
Việc xác định tính đồng biến hay nghịch biến giúp dự đoán xu hướng hàm trong mô hình hóa. Điều đó đặc biệt quan trọng trong bài toán thực tế yêu cầu phân tích xu hướng tăng hay giảm của một đại lượng.

Sự tuyến tính cũng khiến độ thay đổi luôn đều, nghĩa là mức tăng hay giảm không bị biến thiên theo thời gian. Đây là điểm khác biệt nổi bật giữa hàm bậc nhất, các hàm phi tuyến.
Tính liên tục và miền xác định của hàm số bậc nhất
Hàm số bậc nhất là một trong số ít hàm có tính liên tục tuyệt đối trên toàn bộ trục số thực. Không tồn tại bất kỳ giá trị nào của x khiến hàm bị gián đoạn hoặc không xác định.
Điều này được lý giải bởi công thức không chứa căn, phân thức hoặc điều kiện ràng buộc biến. Nhờ vậy, miền xác định của hàm luôn là R, tức tập hợp mọi số thực.
Tính liên tục mang ý nghĩa toán học rằng đồ thị hàm có thể được vẽ bằng một nét không nhấc bút. Mỗi thay đổi nhỏ ở biến số đều kéo theo thay đổi nhỏ tương ứng ở giá trị hàm.
Ngoài ra, không có điểm nhọn, góc gãy hay điểm uốn trên đồ thị của hàm bậc nhất. Điều này khiến việc phân tích hình học trở nên đơn giản, trực quan hơn nhiều so với các loại hàm khác.
Trong các ứng dụng mô phỏng hoặc xử lý số liệu, tính liên tục giúp việc nội suy hay dự đoán không gặp trở ngại. Học sinh cũng dễ dàng chuyển từ bài toán đại số sang hình học một cách mạch lạc.
Mối liên hệ giữa hệ số góc, độ nghiêng
Trong biểu diễn hình học, hệ số aaa không chỉ là con số đại diện cho tốc độ thay đổi mà còn mô tả độ nghiêng của đường thẳng trên mặt phẳng tọa độ. Độ lớn của aaa càng lớn, đường thẳng càng dốc và độ nghiêng càng rõ rệt.
Nếu a=1, đường thẳng tạo với trục hoành một góc 45 độ theo hướng đi lên. Trường hợp a=−1 thì đường thẳng đi xuống cũng với cùng độ nghiêng nhưng ngược chiều.
Khi a tiến gần 0, đường thẳng trở nên gần như nằm ngang, biểu hiện cho hàm có sự thay đổi rất chậm theo biến. Ngược lại, nếu aaa lớn về trị tuyệt đối, độ dốc tăng mạnh, đồ thị trở nên dốc đứng.
Việc xác định hệ số góc không chỉ giúp vẽ nhanh đồ thị mà còn cung cấp cái nhìn tổng quan về tốc độ thay đổi của hàm. Đặc biệt trong các ứng dụng thực tiễn, hệ số góc mang ý nghĩa định lượng rõ ràng.

Ví dụ, trong mô hình vận tốc hoặc tài chính, hệ số aaa đại diện cho tốc độ hoặc mức lãi suất, phản ánh chính xác biến động của đại lượng theo thời gian. Do đó, hiểu đúng bản chất của hệ số góc là yếu tố quyết định trong việc vận dụng hàm số bậc nhất hiệu quả.
Xem thêm: Công Thức Tích Phân – Cách Giải Và Ứng Dụng Thực Tế
Ứng dụng trong các tình huống thực tế
Hàm số bậc nhất không chỉ tồn tại trên sách vở mà còn đóng vai trò quan trọng trong việc mô hình hóa các hiện tượng xung quanh. Từ vận tốc đều đến phân tích dữ liệu, dạng hàm tuyến tính này giúp đơn giản hóa các bài toán đời sống một cách logic, hiệu quả.
Minh họa thực tế trong bài toán chuyển động thẳng đều
Chuyển động thẳng đều là ví dụ kinh điển cho ứng dụng trực tiếp của hàm số bậc nhất trong vật lý phổ thông. Quãng đường di chuyển theo thời gian được biểu diễn qua công thức s=vt+s0, trong đó vận tốc v là hệ số góc.
Khi thời gian tăng đều, quãng đường cũng tăng một cách tuyến tính, không phụ thuộc vào các yếu tố như gia tốc. Đây là trường hợp tiêu biểu cho sự biến thiên đều của một đại lượng theo biến độc lập.
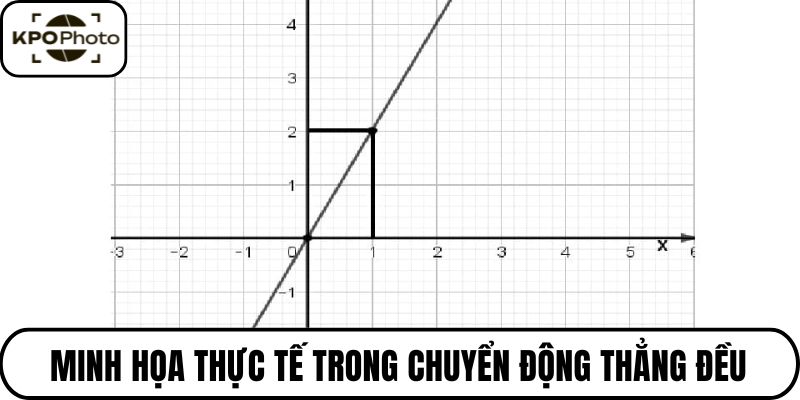
Đồ thị quãng đường theo thời gian là đường thẳng có độ nghiêng phụ thuộc vào giá trị của vận tốc. Vận tốc càng cao, đồ thị càng dốc, thể hiện tốc độ thay đổi quãng đường nhanh hơn.
Thông qua bài toán này, học sinh có thể nhìn thấy mối liên hệ giữa lý thuyết toán học và hiện tượng vật lý. Ngoài ra, việc sử dụng hàm số bậc nhất trong bài toán chuyển động còn hỗ trợ xây dựng các mô phỏng thời gian thực trên phần mềm học tập.
Ứng dụng trong mô hình tài chính đơn giản
Hàm số bậc nhất thường được dùng để biểu diễn lợi nhuận, doanh thu hoặc chi phí trong các mô hình tài chính cơ bản. Một ví dụ phổ biến là công thức tính tổng thu nhập theo số lượng sản phẩm tiêu thụ: T(x)=px+c, với p là giá bán đơn vị.
Trong đó, hệ số p biểu thị tốc độ tăng doanh thu khi số lượng hàng hóa tăng thêm một đơn vị. Phần hằng số ccc có thể là chi phí cố định hoặc khoản lãi ban đầu.
Mối quan hệ tuyến tính giữa biến số và giá trị hàm giúp nhà phân tích dễ dàng dự đoán lợi nhuận theo từng mức đầu tư. Đồng thời, nó còn hỗ trợ xác định điểm hòa vốn khi thu nhập bằng chi phí.
Mô hình dạng này thường là bước đầu trong việc lập kế hoạch tài chính hoặc tối ưu hóa chiến lược kinh doanh. Nhờ tính đơn giản của hàm, người học dễ tiếp cận,phát triển tư duy phân tích dữ liệu định lượng.
Kết luận
Hàm số bậc nhất là nền móng cơ bản nhưng có vai trò rộng lớn trong Đại số và Giải tích. Việc nắm rõ khái niệm, tính chất, ứng dụng kpophoto trình bày không chỉ phục vụ học tập mà còn mở ra khả năng phân tích tình huống thực tế một cách có hệ thống.

